《2025年家庭作业九年级数学上册北师大版》

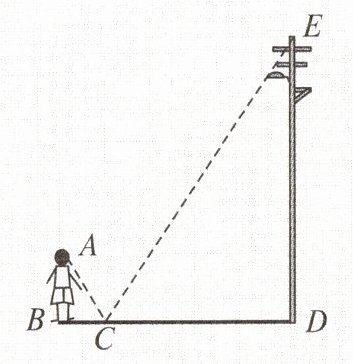
2. 如图，小明在测量电线杆高度的实践活动中，发现地面上有一摊积水，他刚好能从积水中看到电线杆的顶端，测得积水与电线杆底部距离 $ CD = 6m $，他与积水的距离 $ BC = 1m $，他的眼睛距离地面 $ AB = 1.5m $，则电线杆的高度 $ DE $ 是多少米？

答案： 2.解 由题意可知$\angle ABC=\angle EDC=90^{\circ}$,$\angle ACB=\angle ECD$,$\therefore \triangle ABC\sim\triangle EDC$,$\therefore\frac{AB}{ED}=\frac{BC}{DC}$.
$\because CD=6$m,$BC=1$m,$AB=1.5$m,
$\therefore\frac{1.5}{ED}=\frac{1}{6}$,$\therefore DE=9$m.

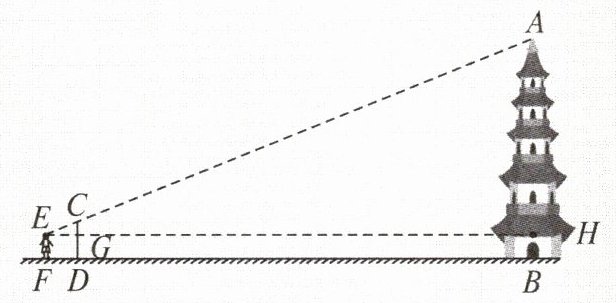
【例题】如图，小明欲测量一座古塔的高度，他拿来一根竹竿竖直插在地面上，然后自己退后，使眼睛通过竹竿的顶端刚好看到塔顶。若小明眼睛离地面 $ 1.6m $，竹竿顶端离地面 $ 2.4m $，小明到竹竿的距离 $ FD = 2m $，竹竿到塔底的距离 $ DB = 33m $，求这座古塔的高度。
思路点拨
(1) 图中线段 $ CG $ 的长是多少？塔高 $ AB $ 等于哪两条线段的和？
(2) $ \triangle EGC $ 与 $ \triangle EHA $ 相似吗？为什么？
听课笔记：

________________________
________________________
________________________

答案： 解 $\because$小明、竹竿、古塔均与地面垂直，$EH\perp AB$,
$\therefore BH=DG=EF=1.6$m,$EG=DF$,$GH=DB$.
$\because$小明眼睛离地面$1.6$m,竹竿顶端离地面$2.4$m,
$\therefore CG=CD-EF=2.4-1.6=0.8$m.
$\because CD// AB$,$\therefore\triangle EGC\sim\triangle EHA$.
$\therefore\frac{AH}{CG}=\frac{EH}{EG}$,即$\frac{AH}{0.8}=\frac{33 + 2}{2}$,解得$AH=14$m.
$\therefore AB=AH+BH=14+1.6=15.6$m.
即这座古塔的高度是$15.6$m.

1. 如图，某校数学兴趣小组利用标杆 $ BE $ 测量建筑物的高度，已知标杆 $ BE $ 高 $ 1.5m $，测得 $ AB = 1.2m $，$ BC = 12.8m $，则建筑物 $ CD $ 的高是(A)。

A.$ 17.5m $
B.$ 17m $
C.$ 16.5m $
D.$ 18m $

答案： 1.A