第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
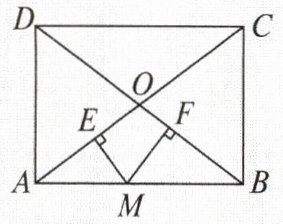
5. 如图,在矩形 $ABCD$ 中,对角线 $AC$,$BD$ 相交于点 $O$,$M$ 是边 $AB$ 上任意一点,$ME \perp AC$ 于点 $E$,$MF \perp BD$ 于点 $F$. $AB = 4$,$BC = 3$,求 $ME + MF$ 的大小.

答案:
5.解:如图,连接OM,过点B作BN⊥AC于点N。

∵四边形ABCD是矩形,
∴∠ABC=90°,AO=$\frac{1}{2}$AC,BO=$\frac{1}{2}$BD,AC=BD,
∴AO=BO。
在Rt△ABC中,AC=$\sqrt{AB^{2}+BC^{2}}$=$\sqrt{4^{2}+3^{2}}$=5。
∵$S_{△AOM}$+$S_{△BOM}$=$S_{△AOB}$=$\frac{1}{2}$$S_{△ABC}$,
即$\frac{1}{2}$OA·ME+$\frac{1}{2}$OB·MF=$\frac{1}{2}$×$\frac{1}{2}$AC·BN,
∴ME+MF=BN=$\frac{AB·BC}{AC}$=$\frac{4×3}{5}$=$\frac{12}{5}$。
5.解:如图,连接OM,过点B作BN⊥AC于点N。

∵四边形ABCD是矩形,
∴∠ABC=90°,AO=$\frac{1}{2}$AC,BO=$\frac{1}{2}$BD,AC=BD,
∴AO=BO。
在Rt△ABC中,AC=$\sqrt{AB^{2}+BC^{2}}$=$\sqrt{4^{2}+3^{2}}$=5。
∵$S_{△AOM}$+$S_{△BOM}$=$S_{△AOB}$=$\frac{1}{2}$$S_{△ABC}$,
即$\frac{1}{2}$OA·ME+$\frac{1}{2}$OB·MF=$\frac{1}{2}$×$\frac{1}{2}$AC·BN,
∴ME+MF=BN=$\frac{AB·BC}{AC}$=$\frac{4×3}{5}$=$\frac{12}{5}$。
1.矩形的判定定理
(1)对角线
(2)有三个角是
温馨提示
与菱形类似,矩形的两个判定定理与它的两个性质定理分别是互逆定理.注意这两种判定方法的起点不同,即一种是基于“平行四边形”的起点而开始判别的,一种是从“四边形”的基础上进行判别的.明确了这些细节,便于我们对矩形判定定理的理解、记忆与应用.
(1)对角线
相等
的平行四边形是矩形.(2)有三个角是
直角
的四边形是矩形.温馨提示
与菱形类似,矩形的两个判定定理与它的两个性质定理分别是互逆定理.注意这两种判定方法的起点不同,即一种是基于“平行四边形”的起点而开始判别的,一种是从“四边形”的基础上进行判别的.明确了这些细节,便于我们对矩形判定定理的理解、记忆与应用.
答案:
1.(1)相等 (2)直角
2.下面检查一个四边形门框是不是矩形的方法中正确的是(
A.用卷尺测量对角线是否互相平分
B.用卷尺测量对角线是否相等
C.用曲尺测量对角线是否互相垂直
D.用曲尺测量门框的三个角是不是直角
D
).A.用卷尺测量对角线是否互相平分
B.用卷尺测量对角线是否相等
C.用曲尺测量对角线是否互相垂直
D.用曲尺测量门框的三个角是不是直角
答案:
2.D
【例题】 如图,将□$ABCD$的边$DC$延长到点$E$,使$CE=DC$,连接$AE$,交$BC$于点$F$.若$\angle AFC=2\angle D$,连接$AC$,$BE$,求证:四边形$ABEC$是矩形.
思路点拨(1)四边形$ABEC$是什么特殊的四边形?
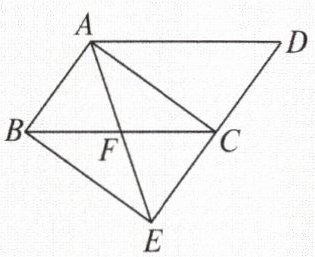
(2)$FB=FA$吗?为什么?由此可用什么方法判定四边形$ABEC$是矩形?
(3)$AE=AD$吗?为什么?由此可用什么方法判定四边形$ABEC$是矩形?
听课笔记:
______________________________
______________________________
思路点拨(1)四边形$ABEC$是什么特殊的四边形?

(2)$FB=FA$吗?为什么?由此可用什么方法判定四边形$ABEC$是矩形?
(3)$AE=AD$吗?为什么?由此可用什么方法判定四边形$ABEC$是矩形?
听课笔记:
证明(方法1)在▱ABCD中,AB=CD,AB//CD.∵CE=DC,∴AB=CE,又AB//CE,∴四边形ABEC是平行四边形.∴AF=EF,BF=CF.在▱ABCD中,∠D=∠ABC.又∠AFC=2∠D,∴∠AFC=2∠ABC=∠ABC+∠BAE,∴∠ABC=∠BAE,∴AF=BF,∴AE=BC.∴▱ABEC是矩形.(方法2)同方法1,可证四边形ABEC是平行四边形.在▱ABCD中,AD//BC,∴∠D=∠BCE.∵∠AFC=2∠D,∴∠AFC=2∠BCE=∠BCE+∠AED,∴∠BCE=∠AED,∴∠D=∠AED,∴AE=AD.∵CE=DC,∴AC⊥DE,∠ACE=90°,∴▱ABEC是矩形.
______________________________
______________________________
答案:
【例题】证明(方法1)在▱ABCD中,AB=CD,AB//CD.
∵CE=DC,
∴AB=CE,又AB//CE,
∴四边形ABEC是平行四边形.
∴AF=EF,BF=CF.
在▱ABCD中,∠D=∠ABC.又∠AFC=2∠D,
∴∠AFC=2∠ABC=∠ABC+∠BAE,
∴∠ABC=∠BAE,
∴AF=BF,
∴AE=BC.
∴▱ABEC是矩形.
(方法2)同方法1,可证四边形ABEC是平行四边形.
在▱ABCD中,AD//BC,
∴∠D=∠BCE.
∵∠AFC=2∠D,
∴∠AFC=2∠BCE=∠BCE+∠AED,
∴∠BCE=∠AED,
∴∠D=∠AED,
∴AE=AD.
∵CE=DC,
∴AC⊥DE,∠ACE=90°,
∴▱ABEC是矩形.
∵CE=DC,
∴AB=CE,又AB//CE,
∴四边形ABEC是平行四边形.
∴AF=EF,BF=CF.
在▱ABCD中,∠D=∠ABC.又∠AFC=2∠D,
∴∠AFC=2∠ABC=∠ABC+∠BAE,
∴∠ABC=∠BAE,
∴AF=BF,
∴AE=BC.
∴▱ABEC是矩形.
(方法2)同方法1,可证四边形ABEC是平行四边形.
在▱ABCD中,AD//BC,
∴∠D=∠BCE.
∵∠AFC=2∠D,
∴∠AFC=2∠BCE=∠BCE+∠AED,
∴∠BCE=∠AED,
∴∠D=∠AED,
∴AE=AD.
∵CE=DC,
∴AC⊥DE,∠ACE=90°,
∴▱ABEC是矩形.
查看更多完整答案,请扫码查看


