《2025年家庭作业九年级数学上册北师大版》

1.在平行四边形$ABCD$中,下列条件:
①$AB=BC$;②$AC=BD$;③$AC\bot BD$;
④$AC$平分$\angle BAD$,其中能说明平行四边形$ABCD$是矩形的是(B).

A.①　　　
B.②　　　
C.③　　　
D.④

答案： 1．B

2.在菱形$ABCD$中,对角线$AC$与$BD$相交于点$O$,再添加下列条件中的(A),仍不能判定四边形$ABCD$是矩形.

A.$AB=AD$
B.$OA=OB$
C.$AC=BD$
D.$DC\bot BC$

答案： 2．A

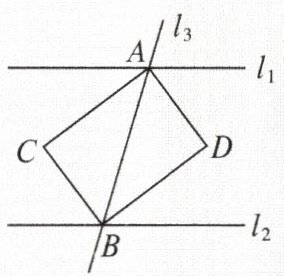
3.已知$l_{1}// l_{2}$,$l_{3}$与$l_{1}$,$l_{2}$分别交于$A$,$B$两点,过$A$,$B$分别作两组内错角的平分线交于$C$,$D$,如图所示,则四边形$ACBD$的形状是矩形.

答案： 3．矩形

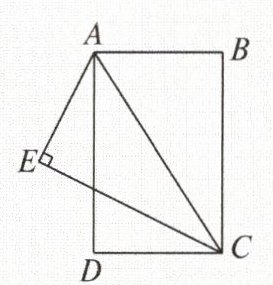
4.如图,已知$BA=AE=DC$,$AD=EC$,$CE\bot AE$,垂足为$E$.
(1)求证:$\triangle DCA\cong \triangle EAC$;
(2)只需添加一个条件,可使四边形$ABCD$为矩形.请写出添加的条件并加以证明.

答案： 4．（1）证明 在△DCA和△EAC中，
∵DC=EA，AD=CE，AC=CA，
∴△DCA≌△EAC．
（2）解 添加条件：AD=BC（条件不唯一），可使四边形ABCD为矩形．证明如下：
∵AB=DC，AD=BC，
∴四边形ABCD是平行四边形．
∵CE⊥AE，
∴∠E=90°．由（1）得，△DCA≌△EAC，
∴∠D=∠E=90°，
∴四边形ABCD为矩形．

1.已知在平行四边形$ABCD$中,$AC$,$BD$是它的两条对角线,则下列条件中,能使这个平行四边形为矩形的是(C).

A.$\angle BAC=\angle DCA$
B.$\angle BAC=\angle DAC$
C.$\angle BAC=\angle ABD$
D.$\angle BAC=\angle ADB$

答案： 1．C