第82页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
2. 小明希望测量出电线杆 $ AB $ 的高度,于是在阳光明媚的一天,他在电线杆旁的点 $ D $ 处立一标杆 $ CD $,使标杆的影子 $ DE $ 与电线杆的影子 $ BE $ 部分重叠(即点 $ E $,$ C $,$ A $ 在一直线上),量得 $ ED = 2 $ 米,$ DB = 4 $ 米,$ CD = 1.5 $ 米。则电线杆 $ AB = $

4.5
米。
答案:
2.4.5
3. 如图,为了测量一棵树 $ CD $ 的高度,测量者在 $ B $ 处竖直立了一根高为 $ 2.8m $ 的标杆,观测者站在 $ F $ 处可以看到杆顶 $ A $、树顶 $ C $ 在同一条直线上,若测得 $ BD = 16m $,$ FB = 4m $,$ EF = 1.6m $,试求树的高度。


答案:
3.解 过点$E$作$EH\perp CD$于点$H$,交$AB$于点$G$,
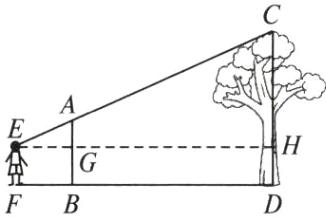
则有$EG = FB$,$GH = BD$,$EF=GB=HD$.
因为$\angle AEG=\angle CEH$,$\angle AGE=\angle CHE=90^{\circ}$,
所以$\triangle EGA\sim\triangle EHC$.
所以$\frac{EG}{EH}=\frac{GA}{HC}$,所以$\frac{4}{4 + 16}=\frac{2.8 - 1.6}{CH}$.
解得$CH = 6$m. 所以树高$CD=CH + HD=6 + 1.6 = 7.6$m.
3.解 过点$E$作$EH\perp CD$于点$H$,交$AB$于点$G$,

则有$EG = FB$,$GH = BD$,$EF=GB=HD$.
因为$\angle AEG=\angle CEH$,$\angle AGE=\angle CHE=90^{\circ}$,
所以$\triangle EGA\sim\triangle EHC$.
所以$\frac{EG}{EH}=\frac{GA}{HC}$,所以$\frac{4}{4 + 16}=\frac{2.8 - 1.6}{CH}$.
解得$CH = 6$m. 所以树高$CD=CH + HD=6 + 1.6 = 7.6$m.
1. 如图,$ AB $ 和 $ CD $ 表示两根直立于地面的柱子,$ AC $ 和 $ BD $ 表示起固定作用的两根钢筋,$ AC $ 与 $ BD $ 相交于点 $ M $,已知 $ AB = 8m $,$ CD = 12m $,则点 $ M $ 离地面的高度 $ MH $ 为(

A.$ 4m $
B.$ \dfrac{24}{5}m $
C.$ 5m $
D.$ \dfrac{16}{3}m $
B
)。
A.$ 4m $
B.$ \dfrac{24}{5}m $
C.$ 5m $
D.$ \dfrac{16}{3}m $
答案:
1.B
2. 如图,数学兴趣小组利用自制的硬纸三角板 $ Rt\triangle ABC $ 来测量操场旗杆 $ MN $ 的高度,他们通过调整测量位置,并使边 $ AC $ 与旗杆顶点 $ M $ 在同一直线上,且 $ Rt\triangle ABC $ 与 $ \triangle AEM $ 在同一个平面内。已知 $ AC = 0.8 $ 米,$ BC = 0.5 $ 米,目测点 $ A $ 到地面的距离 $ AD = 1.5 $ 米,到旗杆的水平距离 $ AE = 20 $ 米,则旗杆 $ MN $ 的高度为

14
米。
答案:
2.14
3. 某单位为了缓解“停车难”的问题,拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图计算 $ CE $。(精确到 $ 0.1m $)


答案:
3.解 由题意知$\angle BAD = 30^{\circ}$.
设$BD=x$m,则$AD = 2x$m.
又$AB = 6$m,$\therefore AD^{2}-BD^{2}=AB^{2}$,
即$(2x)^{2}-x^{2}=6^{2}$,$x = 2\sqrt{3}$.
$\therefore BD = 2\sqrt{3}$m,$AD = 4\sqrt{3}$m.
$\because BC = 1$m,$\therefore CD=BD - BC=(2\sqrt{3}-1)$m.
$\because\angle CED=\angle ABD=90^{\circ}$,$\angle CDE=\angle ADB$,
$\therefore\triangle CDE\sim\triangle ADB$.
$\therefore\frac{CE}{AB}=\frac{CD}{AD}$,即$CE=\frac{2\sqrt{3}-1}{4\sqrt{3}}×6\approx2.1$m.
设$BD=x$m,则$AD = 2x$m.
又$AB = 6$m,$\therefore AD^{2}-BD^{2}=AB^{2}$,
即$(2x)^{2}-x^{2}=6^{2}$,$x = 2\sqrt{3}$.
$\therefore BD = 2\sqrt{3}$m,$AD = 4\sqrt{3}$m.
$\because BC = 1$m,$\therefore CD=BD - BC=(2\sqrt{3}-1)$m.
$\because\angle CED=\angle ABD=90^{\circ}$,$\angle CDE=\angle ADB$,
$\therefore\triangle CDE\sim\triangle ADB$.
$\therefore\frac{CE}{AB}=\frac{CD}{AD}$,即$CE=\frac{2\sqrt{3}-1}{4\sqrt{3}}×6\approx2.1$m.
查看更多完整答案,请扫码查看


