《2025年家庭作业九年级数学上册北师大版》

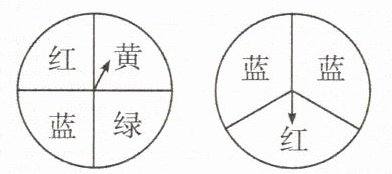
1. 如图，两个转盘分别被分成均匀的4等份和3等份。转动两个转盘各一次，当指针分别指向红色和蓝色时称为配紫色成功，则配紫色成功的概率是(C)。


A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{2}{3}$

答案： 1. C

2. 让图中两个转盘分别自由转动一次，当转盘停止转动时，两个指针分别落在某两个数所表示的区域内，则这两个数的和是2的倍数或是3的倍数的概率等于(C)。


A.$\frac{3}{16}$
B.$\frac{3}{8}$
C.$\frac{5}{8}$
D.$\frac{13}{16}$

答案： 2. C

3. 如图，袋中装有两个大小、质地相同的球，分别标有数字“1”和“2”。小明设计了一个游戏：游戏者每次从袋中随机摸出一个球，并自由转动图中的转盘（转盘被分成相等的三个扇形）。

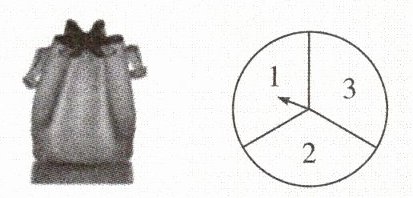
如果所摸球上的数字与转盘转出的数字之和为2，那么游戏者获胜。求游戏者获胜的概率。

答案： 3. 游戏者获胜的概率为$\frac{1}{6}.$

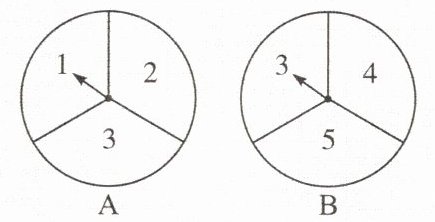
1. 如图，甲、乙两人用这两个转盘(每个转盘被分成相等的3个扇形)做游戏，游戏规则：转动两个转盘各一次，当转盘停止后，指针所在区域的数字之和为偶数时甲获胜；数字之和为奇数时乙获胜。若指针落在分界线上，则需要重新转动转盘。甲获胜的概率是(C)。


A.$\frac{1}{3}$
B.$\frac{4}{9}$
C.$\frac{5}{9}$
D.$\frac{2}{3}$

答案： 1. C

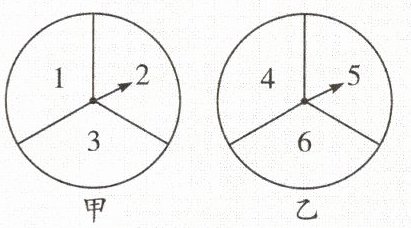
2. 小红和小芳两人在玩转盘游戏，如图，把转盘甲、乙分别分成3等份，并在每一份内标上数字。游戏规则：转动两个转盘，停止后，指针所指的两个数字之和为7时，小红胜；数字之和为8时，小芳胜。则这二人中获胜可能性较大的是小红。

答案： 2. 小红