《2025年家庭作业九年级数学上册北师大版》

3. 在△ABC与△A'B'C'中，AB=6，BC=12，AC=15，A'B'=8，B'C'=16，当A'C'=20时，△ABC∽△A'B'C'.

答案： 3.20

4. 如图，A(1，0)，B(3，0)，C(0，3)，D(2，-1)，P(2，2).

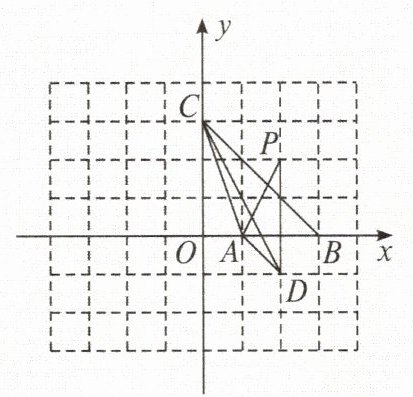
(1)△ABC与△ADP相似吗？请说明理由.
(2)直接写出∠OCA+∠OCD的度数.

答案： 4.
(1)相似.理由略.
(2)$\angle OCA + \angle OCD = 45^{\circ}$.

1. 一般地，点 $ C $ 把线段 $ AB $ 分成两条线段 $ AC $ 和 $ BC $，如果$\frac{AC}{AB}=\frac{BC}{AC}$，那么称线段 $ AB $ 被点 $ C $ 黄金分割，点 $ C $ 叫做线段 $ AB $ 的黄金分割点，$ AC $ 与 $ AB $ 的比叫做黄金比。
温馨提示
黄金分割是指将整体一分为二，较大部分与整体部分的比值等于较小部分与较大部分的比值，其比值约为 $ 0.618 $。这个比例被公认为是最能引起美感的比例，因此被称为黄金分割。一条线段的黄金分割点有两个。黄金三角形是一个等腰三角形，其底与腰的长度比为黄金比值。将一个正五边形的所有对角线连接起来组成五角星，在五角星中可以找到的所有线段之间的长度关系都符合黄金分割比。

答案： 1.$\frac{AC}{AB}=\frac{BC}{AC}$ 黄金分割点

2. 若点 $ M $ 将线段 $ AB $ 黄金分割 $ (AM＞BM) $，则下列各式不正确的是(C)。

A.$ AM:BM = AB:AM $
B.$ AM = \frac{\sqrt{5}-1}{2}AB $
C.$ BM = \frac{\sqrt{5}-1}{2}AB $
D.$ AM \approx 0.618AB $

答案： 2.C