《2025年家庭作业九年级数学上册北师大版》

1. 如图，矩形 $ABCD$ 的面积是 $28$，边 $AB$ 的长比 $AD$ 的长大 $3$，则 $AD$ 的长是4。

答案： 1.4

2. 如图，要利用一面墙（墙长为 $25m$）建羊圈，用 $100m$的围栏围成总面积为 $400m^{2}$的三个大小相同的矩形羊圈，求羊圈的边长 $AB$，$BC$ 各为多少米？（不考虑围栏所占的面积）

答案： 2.羊圈的边长AB,BC都为20m

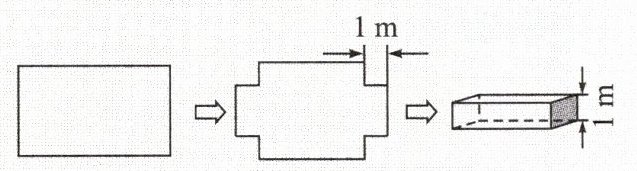
1. 如图，张大叔从市场上买回一块矩形铁皮，他将此矩形铁皮的四个角各剪去一个边长为 $1m$ 的正方形后，剩下的部分刚好能围成一个容积为 $15m^{3}$ 的无盖长方体箱子，且此长方体箱子的底面长比宽多 $2m$。现已知购买这种铁皮每平方米需 $20$ 元钱，张大叔购回这张矩形铁皮共花了(C)。

A.$500$ 元
B.$600$ 元
C.$700$ 元
D.$800$ 元

答案： 1.C

2. 如图，已知线段 $AB$ 的长为 $a$，以 $AB$ 为边在 $AB$ 的下方作正方形 $ACDB$。取 $AB$ 边上一点 $E$，以 $AE$ 为边在 $AB$ 的上方作正方形 $AENM$。过点 $E$ 作 $EF\perp CD$，垂足为 $F$。若正方形 $AENM$ 与四边形 $EFDB$ 的面积相等，则 $AE$ 的长为$\frac{−1+\sqrt{5}}{2}$a。

答案： 2.$\frac{−1+\sqrt{5}}{2}$a

3. 小明准备进行如下操作实验：把一根长 $40cm$ 的铁丝剪成两段，并把每段首尾相连各围成一个正方形。
（1）要使这两个正方形的面积和等于 $58cm^{2}$，小明应该怎么剪这根铁丝？
（2）小明认为这两个正方形的面积之和不可能等于 $48cm^{2}$。你认为他的说法正确吗？请说明理由。

答案： 3.解：
(1)小明应该把铁丝剪成长为12cm和28cm的两段.
(2)设其中一个正方形的边长为ycm，则另一个正方形的边长为(10 - y)cm，由题意得y² + (10 - y)² = 48，整理得y² - 10y + 26 = 0.
∵△ = (-10)² - 4×1×26 = -4＜0，
∴此方程无实数根，即这两个正方形的面积之和不可能等于48cm².故小明的说法是正确的.