《2025年家庭作业九年级数学上册北师大版》

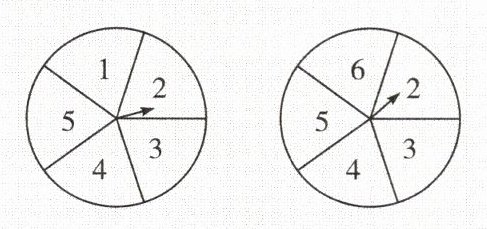
3. 如图，在两个转盘中，指针落在每一个数上的机会都相等，任意转动两个转盘各一次，待其停止后，两个指针所指数的乘积不为6的倍数的概率为$\frac{16}{25}$。

答案： $3. \frac{16}{25}$

4. 如图，一个转盘被等分成三个扇形，上面分别标有$-1$，1，2，指针位置固定，转动转盘后任其自由停止，这时，某个扇形会恰好停在指针所指的位置，并相应得到这个扇形上的数（若指针恰好指在分界线上，当作指向右边的扇形）。

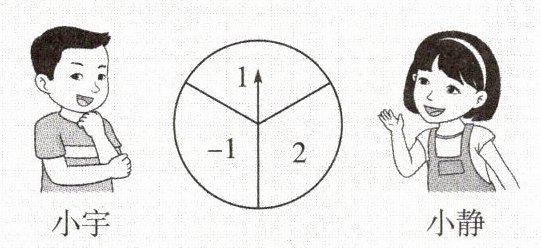
（1）若小静转动转盘一次，求得到负数的概率；
（2）小宇和小静分别转动转盘一次，若两人得到的数相同，则称两人“不谋而合”。用列表法求两人“不谋而合”的概率。

答案： 4. 解
(1)
∵转盘被等分成三个扇形，上面分别标有—1，1,2,
∴小静转动转盘一次，得到负数的概率为$\frac{1}{3}.$
(2)列表如下：
小静
小宇 -1 1 2
-1 (-1,-1) (-1,1) (-1,2)
1 (1,-1) (1,1) (1,2)
2 (2,-1) (2,1) (2,2)
一共有9种等可能的结果，两人得到的数相同的情况有3种，即两人“不谋而合”的概率为$\frac{3}{9}=\frac{1}{3}.$

1. 在进行试验时，当试验的次数很大时，某个事件发生的频率会稳定在相应的概率附近，因此，我们可以通过大量重复试验，用一个事件发生的频率来估计这一事件发生的概率。

答案： 答：在对某个事件进行分析时，依据在大次数重复试验下，事件发生频率稳定于相应概率附近的特性。
具体操作为进行大量重复试验，记录该事件发生的次数$m$以及试验总次数$n$，然后根据公式$P(事件)=\lim_{n \to +\infty} \frac{m}{n}$（这里是用频率估计概率的体现，在大量试验下$\frac{m}{n}$趋近于该事件发生概率），通过计算$\frac{m}{n}$的值来估计这一事件发生的概率。

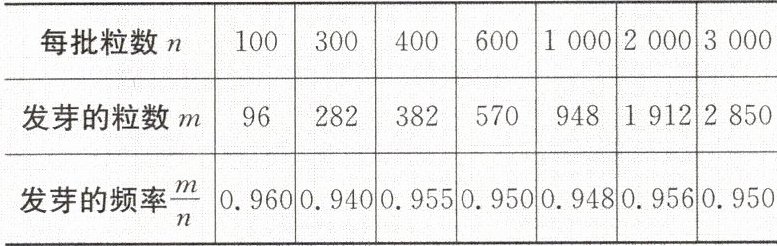
2. 绿豆在相同条件下的发芽试验，结果如表所示：
则绿豆发芽的概率估计值是(B)。

A.0.96
B.0.95
C.0.94
D.0.90

答案： 2.B