《2025年家庭作业九年级数学上册北师大版》

1. 正方形的定义
有一组邻边相等，并且有一个角是直角的平行四边形叫做正方形.

答案： 1.相等　直角

2. 正方形的性质定理
(1)正方形的四个角都是直角，四条边相等.
(2)正方形的对角线相等且互相垂直平分.

答案： 2.
(1)直角　相等　
(2)相等　垂直平分

3. 区分平行四边形、矩形、菱形、正方形的性质
(1)从边来看，它们都具有对边平行且相等的性质，而菱形和正方形还具有四条边相等的性质；
(2)从角来看，它们都具有对角相等且邻角互补的性质，而矩形和正方形还具有四个角都是直角的性质；
(3)从对角线来看，它们都具有对角线互相平分的性质，而矩形与正方形的对角线还具有相等的性质，菱形与正方形的对角线还具有互相垂直的性质.

答案： 3.
(2)直角

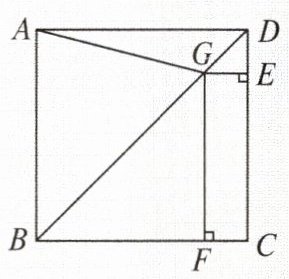
【例题】如图，在正方形ABCD中，点G在对角线BD上(不与点B，D重合)，GE⊥DC于点E，GF⊥BC于点F，连接AG.
(1)写出线段AG，GE，GF长度之间的数量关系，并说明理由；
(2)若正方形ABCD的边长为1，∠AGF=105°，求线段BG的长.
思路点拨 (1)连接GC，△ADG与△CDG全等吗？由此可得线段AG与CG具有什么数量关系？在Rt△GEC中，线段CG，GE，EC有什么数量关系？

(2)作AH⊥BD于点H，则△ABH与△AGH有何特点？BH，HG与BG有何数量关系？
听课笔记：
________________________
________________________
________________________
________________________
________________________
________________________
________________________
________________________

答案：
解
(1)AG²=GE²+GF².

理由如下:连接GC，由正方形的性质知AD=CD，∠ADG=∠CDG.
在△ADG和△CDG中，
∵AD=CD，∠ADG=∠CDG，GD=GD，
∴△ADG≌△CDG，
∴AG=CG.
由题意知∠GEC=∠GFC=∠DCB=90°，
∴四边形GFCE是矩形，
∴GF=EC.
在Rt△GEC中，根据勾股定理，得GC²=GE²+EC²，
∴AG²=GE²+GF².
(2)作AH⊥BD于点H，由题意知∠AGB=60°，∠ABG=45°，
∴△ABH为等腰直角三角形，△AGH为含30°角的直角三角形.

∵AB=1，
∴AH=BH=$\frac{\sqrt{2}}{2}$，HG=$\frac{\sqrt{6}}{6}$，
∴BG=$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{6}}{6}$.