《2025年家庭作业九年级数学上册北师大版》

1. 一般地，如果两个相似多边形任意一组对应顶点$P$，$P'$所在的直线都经过同一个点$O$，且有$OP' = k\cdot OP(k\neq0)$，那么这样的两个多边形叫做位似多边形，点$O$叫做位似中心。实际上，$k$就是这两个相似多边形的相似比。

答案： 1.相似　位似中心　相似比

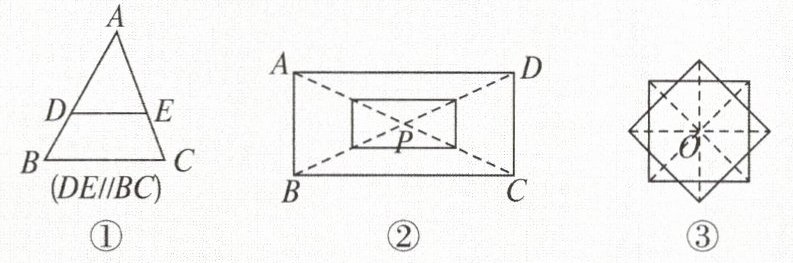
2. 如图，下面3组图形中，位似图形有(C)。


A.0组
B.1组
C.2组
D.3组

答案： 2.C

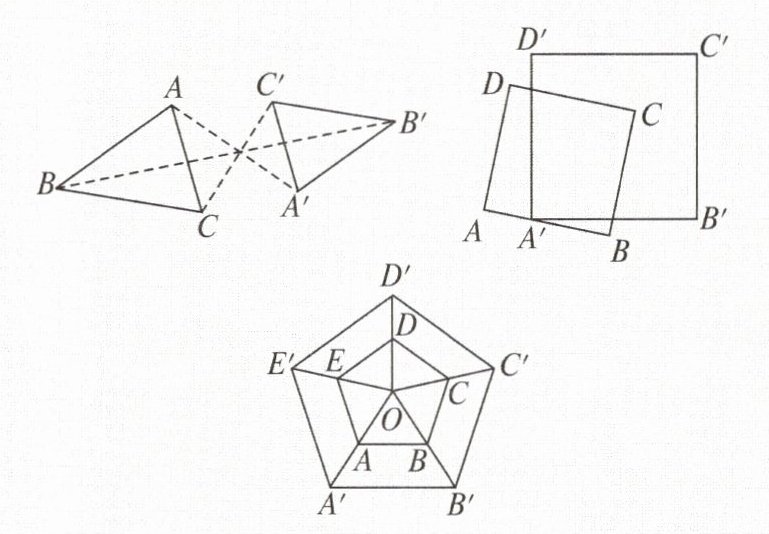
【例1】如图，指出下列各图中的两个图形是不是位似多边形。如果是，请指出其位似中心；如果不是，请说明理由。

思路点拨 判断两个图形是不是位似多边形，首先要看这两个图形是否相似，然后看每组对应点的连线是否都经过同一个点，这两方面缺一不可。
听课笔记：________________________
________________________
________________________
【规律总结】
根据位似多边形的概念，可得到位似多边形的如下性质：位似多边形的任意一对对应点与位似中心在同一条直线上，它们到位似中心的距离之比等于相似比，位似多边形上的对应线段平行或在同一条直线上。

答案： 解题图①,②中的两个多边形都是位似多边形，位似中心分别是题图①中的点A，题图②中的点P.题图③中的点O不是对应点连线的交点，故题图③中的两个多边形不是位似多边形。