《2025年芝麻开花美在课堂高一数学必修第一册北师大版》

通过描述元素满足的条件表示集合的方法叫作描述法.一般可将集合表示为{x及x的范围|x满足的条件},即在花括号内先写出集合中元素的一般符号及范围,再画一条竖线"|",在竖线后写出集合元素所具有的共同特征.

答案： 满足的条件 {x及x的范围|x满足的条件} 共同特征

1. 由大于 $-3$ 且小于 $11$ 的偶数所组成的集合是 (D)
A.$\{x|-3 ＜ x ＜ 11,x \in \mathbf{Z}\}$
B.$\{x|-3 ＜ x ＜ 11\}$
C.$\{x|-3 ＜ x ＜ 11,x = 2k\}$
D.$\{x|-3 ＜ x ＜ 11,x = 2k,k \in \mathbf{Z}\}$

答案： D

2. (多选)集合 $\{1,3,5,7,9\}$ 用描述法可表示为( )

A.$\{x|x$ 是不大于 $9$ 的非负奇数 $\}$
B.$\{x|x = 2k + 1,k \in \mathbf{N}$,且 $k \leqslant 4\}$
C.$\{x|x \leqslant 9,x \in \mathbf{N}_+\}$
D.$\{x|0 \leqslant x \leqslant 9,x \in \mathbf{Z}\}$

答案： AB

3. 用描述法表示下列集合:

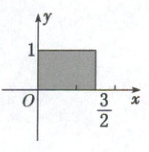
(1) 函数 $y = -2x^2 + x$ 图象上的所有点组成的集合;
(2) 不等式 $2x - 3 ＜ 5$ 的解组成的集合;
(3) 如图中阴影部分的点(含边界)的集合;
(4) $3$ 和 $4$ 的所有正的公倍数构成的集合.

答案：
(1)函数$y=-2x^{2}+x$的图象上的所有点组成的集合可表示为$\{(x,y)|y=-2x^{2}+x\}$.
(2)不等式$2x-3＜5$的解组成的集合可表示为$\{x|2x-3＜5\}$,即$\{x|x＜4\}$.
(3)题图中阴影部分的点(含边界)的集合可表示为$\{(x,y)|0\leqslant x\leqslant \frac{3}{2},0\leqslant y\leqslant 1\}$.
(4)3和4的最小公倍数是12,因此3和4的所有正的公倍数构成的集合是$\{x|x=12n,n\in \mathbf{N}_{+}\}$.

1. 集合的分类

答案： 不含任何元素 ∅ 有限个 无限个

2. 区间
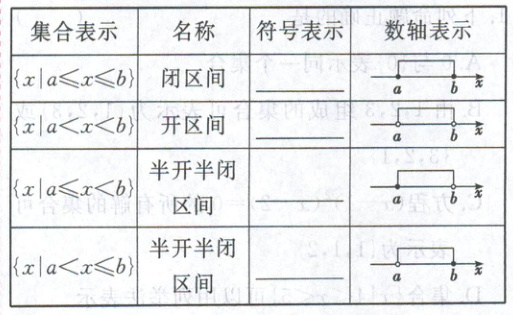
(1) 区间的概念($a,b$ 是两个实数,且 $a ＜ b$)

（2）特殊区间的表示

(1)[a,b]
(2)$(-\infty,+\infty)$ $[a,+\infty)$ $(a,+\infty)$ $(-\infty,b]$ $(-\infty,b)$

答案：
(1)[a,b]
(2)$(-\infty,+\infty)$ $[a,+\infty)$ $(a,+\infty)$ $(-\infty,b]$ $(-\infty,b)$