2025年芝麻开花美在课堂高一数学必修第一册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年芝麻开花美在课堂高一数学必修第一册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第105页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
题点3 对数函数模型
[例4] (2023·新课标Ⅰ卷)(多选)噪声污染问题越来越受到重视.用声压级来度量声音的强弱,定义声压级Lp= 20×lg$\frac{p}{p_{0}}$,其中常数p0(p0>0)是听觉下限阈值,p是实际声压.下表为不同声源的声压级:
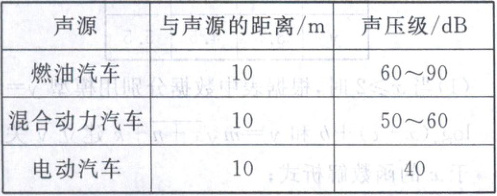
已知在距离燃油汽车、混合动力汽车、电动汽车10m处测得实际声压分别为p1,p2,p3,则(
A.p1≥p2
B.p2>10p3
C.p3= 100p0
D.p1≤100p2
听课记录:
[例4] (2023·新课标Ⅰ卷)(多选)噪声污染问题越来越受到重视.用声压级来度量声音的强弱,定义声压级Lp= 20×lg$\frac{p}{p_{0}}$,其中常数p0(p0>0)是听觉下限阈值,p是实际声压.下表为不同声源的声压级:

已知在距离燃油汽车、混合动力汽车、电动汽车10m处测得实际声压分别为p1,p2,p3,则(
ACD
)A.p1≥p2
B.p2>10p3
C.p3= 100p0
D.p1≤100p2
听课记录:
答案:
选ACD 因为L$_{p}$=20×lg$\frac{p}{p_{0}}$随着p的增大而增大,且L$_{p1}$∈[60,90],L$_{p2}$∈[50,60],所以L$_{p1}$≥L$_{p2}$,所以p$_{1}$≥p$_{2}$,故A正确;由L$_{p}$=20×lg$\frac{p}{p_{0}}$,得p=p$_{0}$10$^{\frac{L_{p}}{20}}$,因为L$_{p3}$=40,所以p$_{3}$=p$_{0}$10$^{\frac{40}{20}}$=100p$_{0}$,故C正确;假设p$_{2}$>10p$_{3}$,则p$_{0}$10$^{\frac{L_{p2}}{20}}$>10p$_{0}$10$^{\frac{L_{p3}}{20}}$,所以10$^{\frac{L_{p2}}{20}-\frac{L_{p3}}{20}}$>10,所以$\frac{L_{p2}-L_{p3}}{20}$>1,所以L$_{p2}$-L$_{p3}$>20,由题中表格数据知不可能成立,故B错误;因为$\frac{100p_{2}}{p_{1}}$=$\frac{100p_{0}10^{\frac{L_{p2}}{20}}}{p_{0}10^{\frac{L_{p1}}{20}}}$=10$^{\frac{L_{p2}}{20}-\frac{L_{p1}}{20}+2}$≥1,所以p$_{1}$≤100p$_{2}$,故D正确. 故选ACD.
2. 记地球与太阳的平均距离为R,地球公转周期为T,万有引力常量为G,则太阳的质量M= $\frac{4π^{2}R^{3}}{GT^{2}}$(单位:kg).由lg$\frac{R^{3}}{GT^{2}}$≈28.7,lg2≈0.3,lgπ≈0.5,计算得太阳的质量约为 (
A.2×1029kg
B.2×1030kg
C.3×1029kg
D.3×1030kg
B
)A.2×1029kg
B.2×1030kg
C.3×1029kg
D.3×1030kg
答案:
选B 由题意在M=$\frac{4π^{2}R^{3}}{GT^{2}}$中两边取对数得,lg M=lg$\frac{R^{3}}{GT^{2}}$+lg 4π²=lg$\frac{R^{3}}{GT^{2}}$+2lg π+2lg 2. 因为lg$\frac{R^{3}}{GT^{2}}$≈28.7,lg 2≈0.3,lg π≈0.5,所以lg M≈28.7+2×0.5+0.3+lg 2=30+lg 2,所以M=10$^{lg M}$=10$^{30+lg 2}$=10$^{lg 2}$×10$^{30}$=2×10$^{30}$. 故选B.
3. 净水机通过分级过滤的方式使自来水逐步达到纯净水的标准,其工作原理中有多次的PP棉滤芯过滤,其中第一级过滤一般由孔径为5微米的PP棉滤芯(聚丙烯熔喷滤芯)构成,其结构是多层式,主要用于去除铁锈、泥沙、悬浮物等各种大颗粒杂质,假设每一层PP棉滤芯可以过滤掉三分之一的大颗粒杂质,若过滤前水中大颗粒杂质含量为80mg/L,现要满足过滤后水中大颗粒杂质含量不超过2mg/L,则PP棉滤芯的层数最少为(参考数据:lg2≈0.30,lg3≈0.48) (
A.9
B.8
C.7
D.6
A
)A.9
B.8
C.7
D.6
答案:
选A 设经过n层PP棉滤芯过滤后的大颗粒杂质含量为y,则y=80×(1-$\frac{1}{3}$)$^{n}$=80×($\frac{2}{3}$)$^{n}$. 令80×($\frac{2}{3}$)$^{n}$≤2,解得($\frac{2}{3}$)$^{n}$≤$\frac{1}{40}$,两边取常用对数得n lg$\frac{2}{3}$≤lg$\frac{1}{40}$,即n lg$\frac{3}{2}$≥lg 40,即n(lg 3-lg 2)≥1+2lg 2. 因为lg 2≈0.30,lg 3≈0.48,所以(0.48-0.30)n≥1.60,解得n≥$\frac{80}{9}$. 因为n∈N$_{+}$,所以n的最小值为9. 故选A.
查看更多完整答案,请扫码查看


