《2025年芝麻开花美在课堂高一数学必修第一册北师大版》

4. 为提高隧道车辆通行能力,研究了隧道内的车流速度v(单位:千米/小时)和车流密度x(单位:辆/千米)所满足的关系式:v= $\begin{cases}50-\frac{x}{6},0＜x≤30,\\65-\frac{k}{160-x},30＜x≤120(k＞0).\end{cases} $研究表明:当隧道内的车流密度达到120辆/千米时造成堵塞,此时车流速度为0千米/小时.
(1)若车流速度v≥40千米/小时,求车流密度x的取值范围;
(2)隧道内的车流量y(单位时间内通过隧道的车辆数,单位:辆/小时)满足y= x·v,求隧道内车流量y的最大值,并指出车流量最大时的车流密度x辆/千米.

答案： 解：
(1)由题意知，当x=120(辆/千米)时，v=0(千米/小时)，代入v=65-$\frac{k}{160-x}$，得k=2 600，所以v=$\begin{cases} 50-\frac{x}{6},0＜x\leqslant30, \\ 65-\frac{2600}{160-x},30＜x\leqslant120. \end{cases}$ 当0＜x≤30时，v=50-$\frac{x}{6}$≥40，易知符合题意；当30＜x≤120时，v=65-$\frac{2600}{160-x}$≥40，解得x≤56，所以30＜x≤56. 综上车流密度x的取值范围是(0,56].
(2)由
(1)知v=$\begin{cases} 50-\frac{x}{6},0＜x\leqslant30, \\ 65-\frac{2600}{160-x},30＜x\leqslant120. \end{cases}$所以当0＜x≤30时，y=x·(50-$\frac{x}{6}$)为增函数，所以y≤1 350，当且仅当x=30等号成立；当30＜x≤120时，y=x·65-$\frac{2600x}{160-x}$=65(x-$\frac{40x}{160-x}$)=65×200-65×[(160-x)+$\frac{6400}{160-x}$]≤13 000-65×2$\sqrt{(160-x)×\frac{6400}{160-x}}$=2 600，即y≤2 600，当且仅当160-x=$\frac{6400}{160-x}$，即x=80时，等号成立. 综上，y的最大值为2 600(辆/小时)，此时x=80(辆/千米). 即隧道内车流量y的最大值为2 600辆/小时，此时车流密度x为80辆/千米.

5. 在无菌培养环境中,某类细菌的繁殖在初期会较快,随着单位体积内细菌数量的增加,繁殖速度又会减慢,在一次实验中,检测到这类细菌在培养皿中的数量y(单位:百万个)与培养时间x(单位:小时)的3组数据如下表所示.

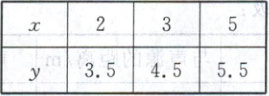
(1)当x≥2时,根据表中数据分别用模型y= loga(x+c)+b和y= m$\sqrt{x+n}$+k建立y关于x的函数解析式;
(2)若用某函数模型根据培养时间来估计某类细菌在培养皿中的数量,则当实际的细菌数量与用函数模型得出的估计值之间的差的绝对值不超过0.5时,称该函数模型为"理想函数模型",已知当培养时间为9小时时,检测到这类细菌在培养皿中的数量为6.2百万个,你认为(1)中哪个函数模型为"理想函数模型"?请说明理由;(参考数据:$\sqrt{57}$≈7.6)
(3)请用(2)中的"理想函数模型"估计17小时后,该类细菌在培养皿中的数量.

答案： 解：
(1)当x≥2时，y=log$_{a}$(x+c)+b，由图表数据可得log$_{a}$(2+c)+b=3.5，log$_{a}$(3+c)+b=4.5，log$_{a}$(5+c)+b=5.5，联立上式，解方程可得a=2，b=3.5，c=-1，则①y=log$_{2}$(x-1)+3.5；当x≥2时，y=m$\sqrt{x+n}$+k，由图表数据可得m$\sqrt{2+n}$+k=3.5，m$\sqrt{3+n}$+k=4.5，m$\sqrt{5+n}$+k=5.5，联立上式，解方程可得m=$\sqrt{2}$，n=-$\frac{15}{8}$，k=3. 则②y=$\sqrt{2}$$\sqrt{x-\frac{15}{8}}$+3.
(2)考虑①y=log$_{2}$(x-1)+3.5，由x=9，可得y=log$_{2}$8+3.5=3+3.5=6.5，而|6.5-6.2|=0.3＜0.5，可得模型①y=log$_{2}$(x-1)+3.5是“理想函数模型”；考虑②y=$\sqrt{2}$$\sqrt{x-\frac{15}{8}}$+3，由x=9，可得y=$\sqrt{2}$×$\sqrt{9-\frac{15}{8}}$+3=$\sqrt{\frac{57}{2}}$+3≈3.8+3=6.8，而|6.8-6.2|=0.6＞0.5，所以模型②不是“理想函数模型”.
(3)由
(2)可得x=17时，y=log$_{2}$(17-1)+3.5=4+3.5=7.5(百万个).