《2025年芝麻开花美在课堂高一数学必修第一册北师大版》

1. 已知 $ m,n \in (0, +\infty) $, $ \frac{1}{m} + n = 4 $,则 $ m + \frac{9}{n} $ 的最小值为 (B)
由题意得m+$\frac{9}{n}$=$\frac{1}{4}$(m+$\frac{9}{n}$)·($\frac{1}{m}$+n)=$\frac{1}{4}$(10+mn+$\frac{9}{mn}$)≥$\frac{1}{4}$(10+2$\sqrt{mn·\frac{9}{mn}}$)=4,当且仅当mn=$\frac{9}{mn}$,即m=1,n=3时等号成立.
A.3
B.4
C.5
D.6

答案： 1.选B 由题意得m+$\frac{9}{n}$=$\frac{1}{4}$(m+$\frac{9}{n}$)·($\frac{1}{m}$+n)=$\frac{1}{4}$(10+mn+$\frac{9}{mn}$)≥$\frac{1}{4}$(10+2$\sqrt{mn·\frac{9}{mn}}$)=4,当且仅当mn=$\frac{9}{mn}$,即m=1,n=3时等号成立.

2. (1) 已知 $ x ＞ 0 $,求 $ 2 - 3x - \frac{4}{x} $ 的最大值;
(2) 已知 $ x ＜ \frac{5}{4} $,求 $ 4x - 2 + \frac{1}{4x - 5} $ 的最大值.
2.解:
(1)因为x＞0,故2-3x-$\frac{4}{x}$=2-(3x+$\frac{4}{x}$)≤2-2$\sqrt{3x·\frac{4}{x}}$=2-4$\sqrt{3}$,当且仅当3x=$\frac{4}{x}$,即x=$\frac{2\sqrt{3}}{3}$时,等号成立,故2-3x-$\frac{4}{x}$的最大值为2-4$\sqrt{3}$.
(2)因为x＜$\frac{5}{4}$,所以5-4x＞0.
所以4x-2+$\frac{1}{4x-5}$=-(5-4x+$\frac{1}{5-4x}$)+3≤-2+3=1,当且仅当5-4x=$\frac{1}{5-4x}$,即x=1时,上式等号成立.
故当x=1时,4x-2+$\frac{1}{4x-5}$的最大值为1.

答案： 2.解:
(1)因为x＞0,故2-3x-$\frac{4}{x}$=2-(3x+$\frac{4}{x}$)≤2-2$\sqrt{3x·\frac{4}{x}}$=2-4$\sqrt{3}$,当且仅当3x=$\frac{4}{x}$,即x=$\frac{2\sqrt{3}}{3}$时,等号成立,故2-3x-$\frac{4}{x}$的最大值为2-4$\sqrt{3}$.
(2)因为x＜$\frac{5}{4}$,所以5-4x＞0.
所以4x-2+$\frac{1}{4x-5}$=-(5-4x+$\frac{1}{5-4x}$)+3≤-2+3=1,当且仅当5-4x=$\frac{1}{5-4x}$,即x=1时,上式等号成立.
故当x=1时,4x-2+$\frac{1}{4x-5}$的最大值为1.

[例4] 如图,动物园要以墙体为背面,用钢筋网围成四间具有相同面积的矩形虎笼. 现有可围 $ 36 \, m $ 长钢筋网的材料,每间虎笼的长、宽各设计为多少时,可使每间 虎笼的面积最大?

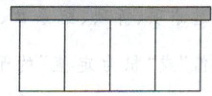
听课记录:
![]
变式拓展
本例条件变为“每间虎笼的面积为 $ 20 \, m^2 $”,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋网总长最小?
[例4] 解:设每间老虎笼的长为x m,宽为y m,则每间老虎笼的面积为S=xy,由已知可得4x+5y=36,由基本不等式可得S=xy=$\frac{1}{20}$·4x·5y≤$\frac{1}{20}$×($\frac{4x+5y}{2}$)²=$\frac{81}{5}$(m²),当且仅当$\left\{\begin{array}{l}4x=5y,\\ 4x+5y=36,\end{array}\right.$即$\left\{\begin{array}{l}x=\frac{9}{2},\\ y=\frac{18}{5}\end{array}\right.$时,等号成立,因此,每间虎笼的长为$\frac{9}{2}$m,宽为$\frac{18}{5}$m时,可使得每间虎笼的面积最大.
[变式拓展]
解:设每间老虎笼的长为x m,宽为y m,则xy=20,钢筋网总长为4x+5y≥2$\sqrt{20xy}$=40(m),当且仅当$\left\{\begin{array}{l}4x=5y,\\ xy=20,\end{array}\right.$即$\left\{\begin{array}{l}x=5,\\ y=4\end{array}\right.$时,等号成立,因此,每间虎笼的长为5 m,宽为4 m时,可使围成四间虎笼的钢筋网总长最小.

答案： [例4] 解:设每间老虎笼的长为x m,宽为y m,则每间老虎笼的面积为S=xy,由已知可得4x+5y=36,由基本不等式可得S=xy=$\frac{1}{20}$·4x·5y≤$\frac{1}{20}$×($\frac{4x+5y}{2}$)²=$\frac{81}{5}$(m²),当且仅当$\left\{\begin{array}{l}4x=5y,\\ 4x+5y=36,\end{array}\right.$即$\left\{\begin{array}{l}x=\frac{9}{2},\\ y=\frac{18}{5}\end{array}\right.$时,等号成立,因此,每间虎笼的长为$\frac{9}{2}$m,宽为$\frac{18}{5}$m时,可使得每间虎笼的面积最大.
[变式拓展]
解:设每间老虎笼的长为x m,宽为y m,则xy=20,钢筋网总长为4x+5y≥2$\sqrt{20xy}$=40(m),当且仅当$\left\{\begin{array}{l}4x=5y,\\ xy=20,\end{array}\right.$即$\left\{\begin{array}{l}x=5,\\ y=4\end{array}\right.$时,等号成立,因此,每间虎笼的长为5 m,宽为4 m时,可使围成四间虎笼的钢筋网总长最小.

3. 制作一个面积为 $ 1 \, m^2 $ 且形状为直角三角形的铁支架,现有 $ 4.6 \, m,4.8 \, m,5 \, m,5.2 \, m $ 四种长度的铁管供选择,较经济(够用,又耗材最少)的是哪一种?

答案： 3.解:设一条直角边长为x,则另一条直角边长是$\frac{2}{x}$,斜边长为$\sqrt{x²+(\frac{2}{x})²}$,故周长C=x+$\frac{2}{x}$+$\sqrt{x²+\frac{4}{x²}}$,由于x+$\frac{2}{x}$≥2$\sqrt{x·\frac{2}{x}}$=2$\sqrt{2}$,且$\sqrt{x²+\frac{4}{x²}}$≥$\sqrt{2\sqrt{x²·\frac{4}{x²}}}$=2,因此C=x+$\frac{2}{x}$+$\sqrt{x²+\frac{4}{x²}}$≥2$\sqrt{2}$+2≈4.83当且仅当x=$\frac{2}{x}$且x²=$\frac{4}{x²}$时,即x=$\sqrt{2}$时等号成立,故较经济(够用,又耗材最少)的是5 m.