《2025年新课标同步单元练习七年级数学上册北师大版深圳专版》

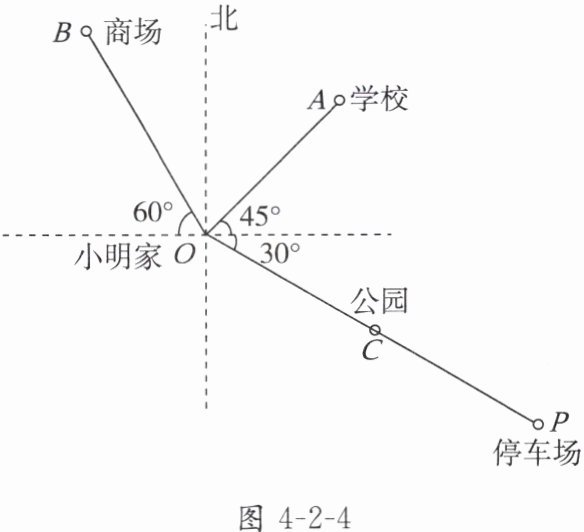
7. 图4-2-4是小明家(图中点O)和学校所在地的简单地图,已知$OA= 2cm$,$OB= 2.5cm$,$OP= 4cm$,C为OP的中点。
(1)请用距离和方向角表示图中商场、学校、公园、停车场分别相对小明家的位置；
(2)若学校距离小明家400m,那么商场和停车场分别距离小明家多少米?

答案： 解：（1）商场在小明家北偏西30°方向，距离2.5 cm位置；学校在小明家北偏东45°方向，距离2 cm位置；公园在小明家南偏东60°方向，距离2 cm位置；停车场在小明家南偏东60°方向，距离4 cm位置。（2）因为学校距离小明家400 m，且OA=2 cm，所以题图中1 cm表示200 m，所以商场距离小明家2.5×200=500（m），停车场距离小明家4×200=800（m）。

1. 若$\angle A$为锐角,$\angle B$为直角,$\angle C$为钝角,请给出$\frac{1}{6}(\angle A+\angle B+\angle C)$的一个可能值,并说明理由。

答案： 解：因为∠A 为锐角，∠B 为直角，∠C 为钝角，所以0°＜∠A＜90°，∠B=90°，90°＜∠C＜180°，所以 $\frac{1}{6}(0^{\circ}+90^{\circ}+90^{\circ})＜\frac{1}{6}(\angle A+\angle B+\angle C)＜\frac{1}{6}(90^{\circ}+90^{\circ}+180^{\circ})$，即30°＜$\frac{1}{6}(\angle A+\angle B+\angle C)$＜60°，在此范围内的值均可。

2. 某同学走进教室发现黑板上面的钟表为$8:30$,他想知道再过多长时间分针能和时针第一次重合。你能帮帮他吗?

答案： 解：因为钟表上一周是360度，有12个大格，所以每个大格的度数为360÷12=30(度)。因为每个大格有5个小格，所以每个小格的度数为30÷5=6(度)。因为1小时是60分钟，每分钟时针走30÷60=0.5(度)，每分钟分针走6度，所以每分钟分针比时针多走5.5度，而且易知时针和分针第一次重合在9时前，8：30时时针与分针的夹角为75度，所以$\frac{75}{5.5}$分钟，即$\frac{150}{11}$分钟后，时针和分针第一次重合。

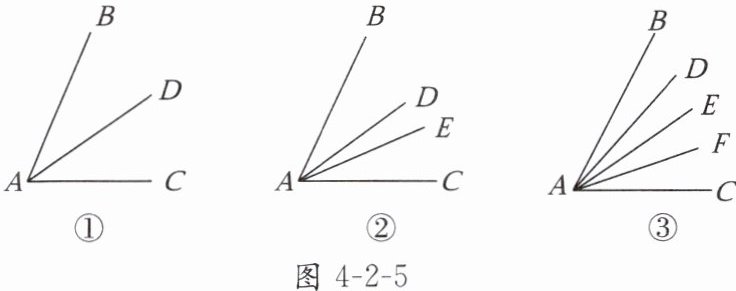
3. (1)如图4-2-5①,如果过角的顶点,在角的内部作一条射线,那么图中一共有几个角?
(2)如图4-2-5②,如果过角的顶点,在角的内部作两条射线,那么图中一共有几个角?
(3)如图4-2-5③,如果过角的顶点,在角的内部作三条射线,那么图中一共有几个角?
(4)如果过角的顶点,在角的内部作n条射线,那么一共有几个角?

答案： （1）如果过角的顶点，在角的内部作一条射线，共有三条射线，那么题图中一共有$\frac{3×2}{2}=3$(个)角。（2）如果过角的顶点，在角的内部作两条射线，共有四条射线，那么题图中一共有$\frac{4×3}{2}=6$(个)角。（3）如果过角的顶点，在角的内部作三条射线，共有五条射线，那么题图中一共有$\frac{5×4}{2}=10$(个)角。（4）如果过角的顶点，在角的内部作n条射线，那么一共有$\frac{(n+2)(n+1)}{2}$个角。