《2025年新课标同步单元练习七年级数学上册北师大版深圳专版》

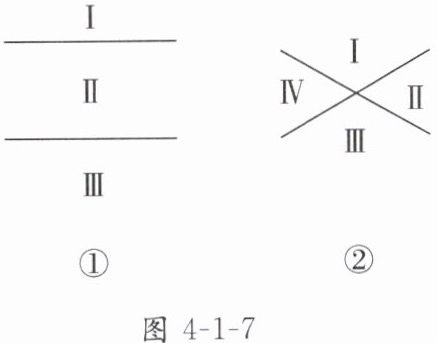
1. 问题：两条直线将平面分成几部分?
解：如图4-1-7①,两条直线平行时,它们将平面分成三部分；
如图4-1-7②,两条直线不平行时,它们将平面分成四部分。
根据上述内容,解答下面的问题。
(1)上面问题的解题过程应用了________的数学思想(填“转化”“分类讨论”“整体处理”或“数形结合”)；
(2)三条直线将平面分成几部分?

答案：

(1)分类讨论
(2)由答图4-1-2①②③④可知，三条直线可以将平面分成四或六或七部分。

2. 在同一平面内,我们把两条直线相交将平面分得的区域数记为$a_{1},$三条直线两两相交最多将平面分得的区域数记为$a_{2},$四条直线两两相交最多将平面分得的区域数记为$a_{3},…,(n + 1)$条直线两两相交最多将平面分得的区域数记为$a_{n}。$$(1)a_{1}=$4$,a_{2}=$7$,a_{3}=$11；$(2)a_{n}=$$\frac{(n+1)(n+2)}{2}+1$；(3)求$\frac{1}{a_{1}-1}+\frac{1}{a_{2}-1}+…+\frac{1}{a_{n}-1}。$(当n为正整数时$,1 + 2 + 3 + … + n= \frac{n(n + 1)}{2})\frac{1}{a_{1}-1}+\frac{1}{a_{2}-1}+…+\frac{1}{a_{n}-1}=\frac{1}{1+2}+\frac{1}{1+2+3}+…+\frac{1}{1+2+3+…+(n+1)}=\frac{2}{(1+2)×2}+\frac{2}{(1+3)×3}+…+\frac{2}{(1+n+1)(n+1)}=2\left[\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{(n+1)(n+2)}\right]=2\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{n+1}-\frac{1}{n+2}\right)=2\left(\frac{1}{2}-\frac{1}{n+2}\right)=\frac{n}{n+2}。$

答案：
(1)4 7 11
(2)$\frac{(n+1)(n+2)}{2}+1$
(3)$\frac{1}{a_{1}-1}+\frac{1}{a_{2}-1}+\cdots+\frac{1}{a_{n}-1}=\frac{1}{1+2}+\frac{1}{1+2+3}+\cdots+\frac{1}{1+2+3+\cdots+(n+1)}$$=\frac{2}{(1+2)×2}+\frac{2}{(1+3)×3}+\cdots+\frac{2}{(1+n+1)(n+1)}$$=2\left[\frac{1}{2×3}+\frac{1}{3×4}+\cdots+\frac{1}{(n+1)(n+2)}\right]$$=2\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\cdots+\frac{1}{n+1}-\frac{1}{n+2}\right)$$=2\left(\frac{1}{2}-\frac{1}{n+2}\right)$$=\frac{n}{n+2}$。

3. (1)试验探索：
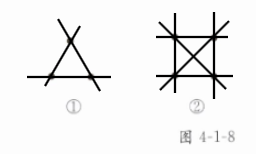
在图4-1-8中过任意两点画直线,并回答问题：

在图4-1-8①中,过任意两点总共能画3条直线；在图4-1-8②中,过任意两点总共能画6条直线；在图4-1-8③中,过任意两点总共能画10条直线。
(2)归纳结论：
如果平面上有$n(n\geq3)$个点,且任意3个点均不在同一条直线上,那么经过任意两点总共能画$\frac{n(n-1)}{2}$条直线。(用含$n$的代数式表示)
(3)解决问题：
某班45名同学在毕业后的一次聚会中,若每两人握一次手问好,则共握多少次手?最后每两人互赠礼物留念,则共需多少件礼物?
$\frac{1}{2}×45×(45-1)=990$(次)，$990×2=1980$(件)。所以若每两人握一次手问好，则共握990次手；若每两人互赠礼物留念，则共需1980件礼物。

答案：

(1)
3 6 10
(2)$\frac{n(n-1)}{2}$
(3)$\frac{1}{2}×45×(45-1)=990$(次)，$990×2=1980$(件)。所以若每两人握一次手问好，则共握990次手；若每两人互赠礼物留念，则共需1980件礼物。