《2025年新课标同步单元练习七年级数学上册北师大版深圳专版》

4. 若$x$的相反数是2,$|y| = 5$,则$x + y$的值为3或-7。

答案： 3或-7

5. 设$[x]表示不超过x$的最大整数,如：$[1.99] = 1$,$[-1.02] = -2$,则$[-1.8] + [3.2] = $1。

答案： 1

6. 计算：
(1)$(-11) + 0$；
(2)$(-6) + (-7)$；
(3)$51 + (-25)$；
(4)$(-12) + 5$；
(5)$(-1.1) + (-2.9)$；
(6)$(-\frac{4}{5}) + \frac{2}{3}$。

答案： 解：
(1)(-11)+0
=-11；
(2)(-6)+(-7)
=-(6+7)
=-13；
(3)51+(-25)
=+(51-25)
=26；
(4)(-12)+5
=-(12-5)
=-7；
(5)(-1.1)+(-2.9)
=-(1.1+2.9)
=-4；
(6)$(-\frac{4}{5})+\frac{2}{3}$
$=(-\frac{12}{15})+\frac{10}{15}$
$=-(\frac{12}{15}-\frac{10}{15})$
$=-\frac{2}{15}$。

7. 小明在一条南北走向的街道上,先向南走了30m,然后又向北走了50m,你能确定他现在位于原出发位置的哪个方向吗？与原出发位置相距多少米？

答案： 解：小明先向南走了30 m，实际是向北走了-30 m，然后又向北走了50 m，所以他现在位于原出发位置的北边，与原出发位置相距50+(-30)=20(m)。

1. 有理数$a$,$b$在数轴上的对应点的位置如图2-2-2所示,用“$＞$”“$＜$”或“$=$”填空。

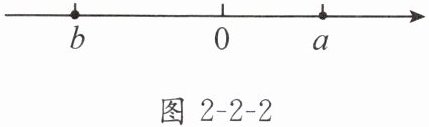
(1)$a + b$＜$0$；
(2)$a + (-b)$＞$0$；
(3)$(-a) + b$＜$0$；
(4)$(-a) + (-b)$＞$0$。

答案：
(1)＜
(2)＞
(3)＜
(4)＞

2. 我们学习了有理数的相关运算,在探究“有理数加法法则”的过程中,我们只要通过对几类运算进行归纳总结,就可以得出该法则。
(1)下列给出的算式中：①$3 + (-2)$；②$4 + 3$；③$(-3) + (-2)$；④$3 + \frac{1}{3}$；⑤$3 + 0$；⑥$6 + (-3)$；⑦$(-5) + 4$；⑧$5 + (-5)$。你认为可以帮助探究有理数加法法则的算式组合是(C)。
A. ①②③④⑤⑧
B. ①②④⑤⑦⑧
C. ②③⑤⑥⑦⑧
D. ①③④⑤⑥⑧
(2)当$a ＞ b$时,若有$a + b ＞ 0$,请说明$a$,$b$需要满足的条件。

答案：
(1)C
解析：根据②④得出两个正数相加，根据③得出两个负数相加，根据⑤得出任何数和0相加，根据①⑥得出一个正数和一个负数相加，其中正数的绝对值比负数的绝对值大，根据⑦得出一个负数和一个正数相加，其中负数的绝对值比正数的绝对值大，根据⑧得出互为相反数的两数相加。故选C。
(2)分为三种情况：①当a＞b≥0时，a，b在取值范围内任意取值，都有a+b＞0；
②当a＞0＞b，|a|＞|b|时，有a+b＞0；
③当0＞a＞b时，无论a，b取何值，都无法得到a+b＞0。