《2025年新课标同步单元练习七年级数学上册北师大版深圳专版》

2. 探索研究：
【观察发现】比较下列各式的大小。(用“＞”“＜”或“=”填空)
①|-2|+|3|＞|-2 + 3|；
②$\left\vert -\frac{1}{2}\right\vert +\left\vert -\frac{1}{3}\right\vert$=$\left\vert -\frac{1}{2}-\frac{1}{3}\right\vert$；
③|6|+|-3|＞|6 - 3|；
④|0|+|-8|=|0 - 8|。
【类比归纳】通过以上比较,请你分析、归纳出当a,b为有理数时,|a|+|b|与|a + b|的大小关系为|a|+|b|≥|a+b|(直接写出结论即可)。
【实践应用】如果|a₁ + a₂|+|a₃ + a₄| = 12,|a₁ + a₂ + a₃ + a₄| = 2,那么a₁ + a₂ = 7或-7或5或-5。

答案： 【观察发现】①＞
解析：因为|-2|+|3|=5，|-2+3|=1，所以|-2|+|3|＞|-2+3|。
②=
解析：因为$\left|-\frac{1}{2}\right|+\left|-\frac{1}{3}\right|=\frac{5}{6}$，$\left|-\frac{1}{2}-\frac{1}{3}\right|=\frac{5}{6}$，所以$\left|-\frac{1}{2}\right|+\left|-\frac{1}{3}\right|=\left|-\frac{1}{2}-\frac{1}{3}\right|$。
③＞
解析：因为|6|+|-3|=9，|6-3|=3，所以|6|+|-3|＞|6-3|。
④=
解析：因为|0|+|-8|=8，|0-8|=8，所以|0|+|-8|=|0-8|。
【类比归纳】|a|+|b|≥|a+b|
解析：分三种情况讨论：
当a，b异号时，|a|+|b|＞|a+b|；
当a，b同号时，|a|+|b|=|a+b|；
当a=0或b=0时，|a|+|b|=|a+b|。
综上所述，|a|+|b|≥|a+b|。
故|a|+|b|与|a+b|的大小关系为|a|+|b|≥|a+b|。
【实践应用】7或-7或5或-5
解析：由|a₁+a₂|+|a₃+a₄|=12，|a₁+a₂+a₃+a₄|=2，可得a₁+a₂和a₃+a₄异号，则a₁+a₂=7或-7或5或-5。

3. 我们可以利用数、形来表示数量关系。
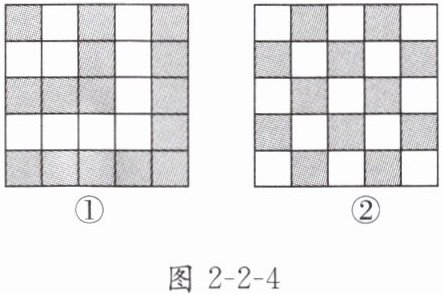
(1)对于“$1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25$”,用下列图形(如图$2 - 2 - 4$)______(填序号)可以最直观得到结论；

(2)对于“$2 + 4 + 6 + 8 = 20$”,请画出可最直观得到此结论的图形；
(3)计算$8 + 4 + 2 + 1 + \frac{1}{2} + \frac{1}{4} = $______,请画出图形,并结合图形说明该结论成立。

答案：

(1)②
(2)(答案不唯一)
方法一(如答图2-2-1)：
　　　　　
方法二(如答图2-2-2)：
　　　　　　　　
(3)$15\frac{3}{4}$
示意图如答图2-2-3所示(答案不唯一)：
　　　　　　　
画边长为4的正方形，依次分割其面积的一半，即8，4，2，1，$\frac{1}{2}$，$\frac{1}{4}$，最后剩余面积$\frac{1}{4}$，则有$8+4+2+1+\frac{1}{2}+\frac{1}{4}=16-\frac{1}{4}=15\frac{3}{4}$。