第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
7. 梳理本章内容,用适当的方式呈现全章知识结构,并与同伴交流。
答案:
本章主要内容包括有理数的相关概念、运算及应用。
一、有理数的概念
1. 有理数的定义:整数(正整数、0、负整数)和分数(正分数、负分数)统称为有理数。
2. 数轴:规定了原点、正方向和单位长度的直线。任何一个有理数都可以用数轴上的一个点来表示。
3. 相反数:只有符号不同的两个数互为相反数。0的相反数是0。若a、b互为相反数,则a + b = 0。
4. 绝对值:数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|。正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是0。即:|a| = a(a > 0);|a| = 0(a = 0);|a| = -a(a < 0)。
5. 有理数的大小比较:正数大于0,负数小于0,正数大于负数;两个负数,绝对值大的反而小。
二、有理数的运算
1. 有理数的加法
同号两数相加,取相同的符号,并把绝对值相加。
异号两数相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值。
一个数同0相加,仍得这个数。
加法交换律:a + b = b + a;加法结合律:(a + b) + c = a + (b + c)。
2. 有理数的减法:减去一个数,等于加上这个数的相反数。即a - b = a + (-b)。
3. 有理数的乘法
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。
几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数。
乘法交换律:a×b = b×a;乘法结合律:(a×b)×c = a×(b×c);乘法分配律:a×(b + c) = a×b + a×c。
4. 有理数的除法
除以一个不等于0的数,等于乘这个数的倒数。即a÷b = a×(1/b)(b≠0)。
两数相除,同号得正,异号得负,并把绝对值相除。0除以任何一个不等于0的数,都得0。
5. 有理数的乘方:求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂。在aⁿ中,a叫做底数,n叫做指数。正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何正整数次幂都是0。
6. 有理数的混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,从左到右进行;如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行。
三、科学记数法与近似数
1. 科学记数法:把一个大于10的数表示成a×10ⁿ的形式(其中1≤a<10,n是正整数),这种记数方法叫做科学记数法。
2. 近似数:接近实际数目,但与实际数目还有差别的数叫做近似数。一般地,一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位。
一、有理数的概念
1. 有理数的定义:整数(正整数、0、负整数)和分数(正分数、负分数)统称为有理数。
2. 数轴:规定了原点、正方向和单位长度的直线。任何一个有理数都可以用数轴上的一个点来表示。
3. 相反数:只有符号不同的两个数互为相反数。0的相反数是0。若a、b互为相反数,则a + b = 0。
4. 绝对值:数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|。正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是0。即:|a| = a(a > 0);|a| = 0(a = 0);|a| = -a(a < 0)。
5. 有理数的大小比较:正数大于0,负数小于0,正数大于负数;两个负数,绝对值大的反而小。
二、有理数的运算
1. 有理数的加法
同号两数相加,取相同的符号,并把绝对值相加。
异号两数相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值。
一个数同0相加,仍得这个数。
加法交换律:a + b = b + a;加法结合律:(a + b) + c = a + (b + c)。
2. 有理数的减法:减去一个数,等于加上这个数的相反数。即a - b = a + (-b)。
3. 有理数的乘法
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。
几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数。
乘法交换律:a×b = b×a;乘法结合律:(a×b)×c = a×(b×c);乘法分配律:a×(b + c) = a×b + a×c。
4. 有理数的除法
除以一个不等于0的数,等于乘这个数的倒数。即a÷b = a×(1/b)(b≠0)。
两数相除,同号得正,异号得负,并把绝对值相除。0除以任何一个不等于0的数,都得0。
5. 有理数的乘方:求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂。在aⁿ中,a叫做底数,n叫做指数。正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何正整数次幂都是0。
6. 有理数的混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,从左到右进行;如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行。
三、科学记数法与近似数
1. 科学记数法:把一个大于10的数表示成a×10ⁿ的形式(其中1≤a<10,n是正整数),这种记数方法叫做科学记数法。
2. 近似数:接近实际数目,但与实际数目还有差别的数叫做近似数。一般地,一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位。
8. 如图 1 - 5 所示,木工师傅把一根长为 1.6 m 的长方体木料沿与左侧面平行的方向锯成 3 段后,表面积比原来增加了$ 80 cm^2,$那么这根长方体木料原来的体积是多少?


答案:
解:因为把长方体木料沿与左侧面平行的方向锯成3段后,其表面积增加了四个截面的面积和,所以每个截面的面积为80÷4=20(cm²),所以这根长方体木料原来的体积是1.6×100×20=3 200(cm³)。
1. 用 10 个大小相同的棱长是 1 cm 的小立方体组成如图 1 - 6 所示的几何体,那么这个几何体的表面积为

36 cm²
。
答案:
36 cm²
2. 现有一个表面涂满颜色的正方体,如图 1 - 7,将每条棱都四等分,再把它切开变成若干个小正方体,则其中三面都涂色的有

8
个,两面都涂色的有24
个,只有一面涂色的有24
个,各面都没有涂色的有8
个。
答案:
8 24 24 8
3. 【项目式学习】
项目主题:包装纸盒的设计。
项目内容:精美的包装总是能让人心情愉悦,市场上的包装更是多种多样,学会用数学的眼光看世界,某学习小组结合“丰富的图形世界”的学习,开展了一次设计之旅。
任务一:图 1 - 8 中的三个几何体是市场上常见的包装模型,请分别写出每种包装对应的几何体的名称。

(1)几何体:①______②______③正三棱柱
任务二:现将 6 瓶某饮料用任务一中的三个几何体分别进行包装,每瓶该饮料近似看作一个圆柱,该饮料每瓶高约是 14 cm,底面圆半径约是 6 cm,图 1 - 9①②③分别是 6 瓶该饮料分别用几何体①、几何体②、几何体③包装后从上面看到的形状图。
(2)图 1 - 9①的形状图中长方形的面积是______ $cm^{2}$;
(3)量得图 1 - 9②中大圆的半径约是 18 cm,请写出用几何体②包装的侧面积:______ $cm^{2}$(结果保留 π);
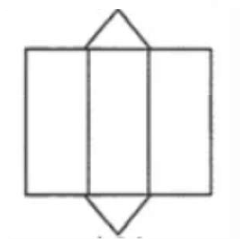
(4)请画出图 1 - 9③对应几何体的其中一种表面展开图。

项目主题:包装纸盒的设计。
项目内容:精美的包装总是能让人心情愉悦,市场上的包装更是多种多样,学会用数学的眼光看世界,某学习小组结合“丰富的图形世界”的学习,开展了一次设计之旅。
任务一:图 1 - 8 中的三个几何体是市场上常见的包装模型,请分别写出每种包装对应的几何体的名称。

(1)几何体:①______②______③正三棱柱
任务二:现将 6 瓶某饮料用任务一中的三个几何体分别进行包装,每瓶该饮料近似看作一个圆柱,该饮料每瓶高约是 14 cm,底面圆半径约是 6 cm,图 1 - 9①②③分别是 6 瓶该饮料分别用几何体①、几何体②、几何体③包装后从上面看到的形状图。
(2)图 1 - 9①的形状图中长方形的面积是______ $cm^{2}$;
(3)量得图 1 - 9②中大圆的半径约是 18 cm,请写出用几何体②包装的侧面积:______ $cm^{2}$(结果保留 π);
(4)请画出图 1 - 9③对应几何体的其中一种表面展开图。

答案:
解:
(1)①长方体 ②圆柱
(2)864
(3)504π
(4)
解:
(1)①长方体 ②圆柱
(2)864
(3)504π
(4)

查看更多完整答案,请扫码查看


