第90页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 小南同学报名参加了南开中学的攀岩选修课,攀岩墙近似一个长方体的两个侧面,如图所示,他根据学过的数学知识准确地判断出:从点A攀爬到点B的最短路径为(
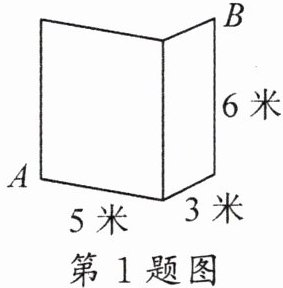
A.6米
B.8米
C.10米
D.14米
C
)
A.6米
B.8米
C.10米
D.14米
答案:
C
2. 如图,有一圆柱形油罐,已知:油罐的底面周长是12m,高AB是5m,要从A点环绕油罐建梯子,正好到A点的正上方B点,梯子最短需要(
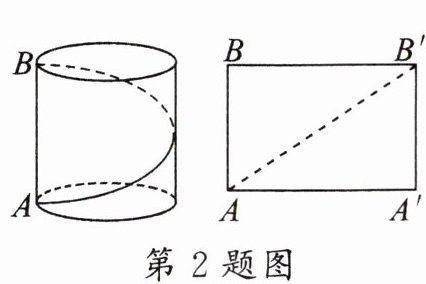
A.12m
B.13m
C.17m
D.20m
B
)
A.12m
B.13m
C.17m
D.20m
答案:
B
3. 如图,有一个木质正方体装饰品,其棱长为2cm,B为一条棱的中点. 小明同学想从点A经过棱CD到点B修饰一条纹路,则纹路的最短距离是多少?
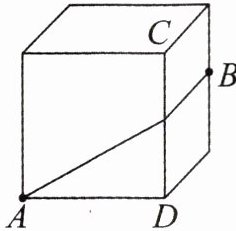

答案:
解:将正方体表面展开如图,

由正方形的性质和直角三角形的性质可得
AE=2×2=4(cm),BE=$\frac{1}{2}$×2=1(cm),则修饰纹路的最短距离为AB=$\sqrt{AE^2+BE^2}$=$\sqrt{4^2+1^2}$=$\sqrt{17}$cm.
解:将正方体表面展开如图,

由正方形的性质和直角三角形的性质可得
AE=2×2=4(cm),BE=$\frac{1}{2}$×2=1(cm),则修饰纹路的最短距离为AB=$\sqrt{AE^2+BE^2}$=$\sqrt{4^2+1^2}$=$\sqrt{17}$cm.
4. (教材练习题变式)如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点A,B之间的距离是(
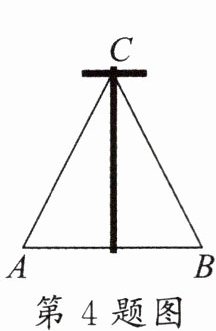
A.13
B.9
C.18
D.10
C
)
A.13
B.9
C.18
D.10
答案:
C
5. (教材例题变式)一辆装满货物,宽为2.4米的卡车,欲通过如图所示的隧道(上方为半圆形),则卡车的外形高必须低于(
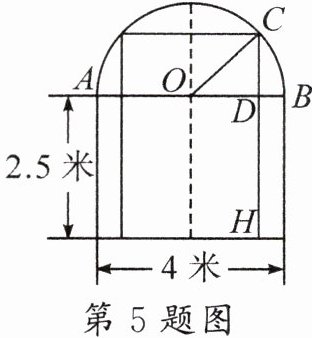
A.4.1米
B.4.0米
C.3.9米
D.3.8米
A
)
A.4.1米
B.4.0米
C.3.9米
D.3.8米
答案:
A
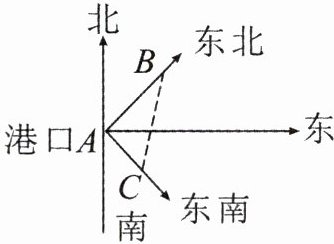
6. 如图所示,一轮船以8n mile/h的速度从港口A出发向东北方向航行,另一轮船以6n mile/h的速度同时从港口A出发向东南方向航行,那么离开港口2h后,两船相距多远?

答案:
解:
∵两船分别沿东北及东南方向行驶,
∴∠BAC=90°,
设2小时后沿东北方向行驶的轮船到达B点,沿东南方向行驶的轮船到达C点,连结BC,
∴AB=8×2=16nmile,AC=6×2=12nmile,
∴BC=$\sqrt{AB^2+AC^2}$=$\sqrt{16^2+12^2}$=20nmile.
答:离开港口A2h后,两船相距20nmile.
∵两船分别沿东北及东南方向行驶,
∴∠BAC=90°,
设2小时后沿东北方向行驶的轮船到达B点,沿东南方向行驶的轮船到达C点,连结BC,
∴AB=8×2=16nmile,AC=6×2=12nmile,
∴BC=$\sqrt{AB^2+AC^2}$=$\sqrt{16^2+12^2}$=20nmile.
答:离开港口A2h后,两船相距20nmile.
查看更多完整答案,请扫码查看


