《2025年黄冈金牌之路练闯考八年级数学上册华师大版》

10. (平顶山期末)下面是投影屏上展示的抢答题,需要回答横线上符号代表的内容,下列回答正确的是(C)

A.$\odot$ 代表 $\angle FEC$
B.$□$ 代表同位角
C.$\blacktriangle$ 代表 $\angle EFC$
D.$\ast$ 代表 $AB$

答案： C

11. 新情境 趣味数学 甲、乙、丙三个同学中,有一位在同学们都不在时把教室扫净,事后老师问他们是谁做的好事,甲说：“是乙做的”；乙说：“不是我做的”；丙说：“不是我做的”.如果他们中有两人说的是假话,一人说的是真话,你能判断是谁做的吗？(C)
A.甲
B.乙
C.丙
D.无法判断

答案： C

12. 如图,将三个正方形的一个顶点重合放置,则 $\angle 1+\angle 2+\angle 3$ 等于90°.

答案： 90°

13. 如图,$DP$ 平分 $\angle ADC$ 交 $AB$ 于点 $P$,$\angle DPC = 90^{\circ}$,如果 $\angle 1+\angle 3 = 90^{\circ}$,那么 $\angle 2$ 和 $\angle 4$ 相等吗？说明理由.
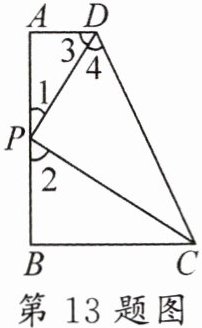
解：$\because DP$ 平分 $\angle ADC$,$\therefore\angle 3= $4.(角平分线定义)
$\because\angle APB= $180°,且 $\angle DPC = 90^{\circ}$,$\therefore\angle 1+\angle 2 = 90^{\circ}$.
又 $\because\angle 1+\angle 3 = 90^{\circ}$,$\therefore\angle 2= \angle 3$,(等角的余角相等)$\therefore\angle 2= \angle 4$.

答案： 4 角平分线定义 180° 等角的余角相等

14. (教材练习变式)图①是王师傅制作的一个模具,按规定 $BA$,$CD$ 的延长线的夹角 $\angle 1$ 应为 $60^{\circ}$,王师傅测得 $\angle B = 45^{\circ}$,$\angle C = 75^{\circ}$.
(1)王师傅制作的模具符合要求吗？请通过计算说明理由；
(2)判断所依据的数学定理是：______；
(3)根据(2)中定理的条件和结论画出了如图②所示的图形,补全求证及定理的证明过程.
已知：$\triangle ABC$.
求证：$\angle BAC+\angle B+$______$=$______.
证明：过点 $A$ 作 $EF// BC$.

(1)王师傅制作的模具符合要求.理由如下:∵∠B=45°,∠C=75°,∴∠1=180°-45°-75°=60°；
(2)三角形内角和定理(三角形内角和为180°)；
(3)∠C180°∴∠B=∠BAE,∠C=∠CAF,∴∠B+∠C=∠BAE+∠CAF.∵∠BAE+∠CAF+∠BAC=180°,∴∠BAC+∠B+∠C=180°.

答案：
(1)王师傅制作的模具符合要求.理由如下:
∵∠B=45°,∠C=75°,
∴∠1=180°-45°-75°=60°;
(2)三角形内角和定理(三角形内角和为180°);
(3)已知:△ABC.求证:∠BAC+∠B+∠C=180°.证明:过点A作EF//BC,
∴∠B=∠BAE,∠C=∠CAF,
∴∠B+∠C=∠BAE+∠CAF.
∵∠BAE+∠CAF+∠BAC=180°,
∴∠BAC+∠B+∠C=180°.