第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
9. 如图,在Rt△ABC中,∠C= 90°,∠BAC= 50°,则根据图中尺规作图的痕迹可知,∠ADB的度数为(
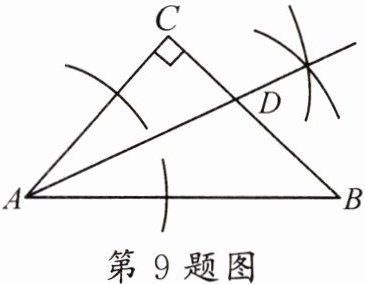
A.140°
B.130°
C.125°
D.115°
D
)
A.140°
B.130°
C.125°
D.115°
答案:
D
10. (信阳校级月考)如图,AD是△ABC的角平分线,DE⊥AB于点E,若$S_{△ABC}= 9$,AB= 5,DE= 2,则AC的长为(
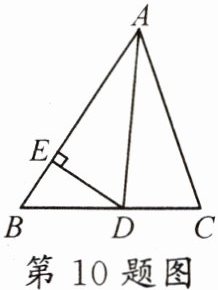
A.5
B.4
C.3
D.2
B
)
A.5
B.4
C.3
D.2
答案:
B
11. (枫杨外国语学校月考)如图,在△ABC中,∠C= 90°,AD平分∠BAC,DE⊥AB于点E,BE= 2,BC= 6,∠B= 40°,则∠DAB=

22.5°
,△BDE的周长是 。
答案:
22.5°
12. 新情境 创新设题 如图①是一个平分角的仪器,其中OD= OE,FD= FE。
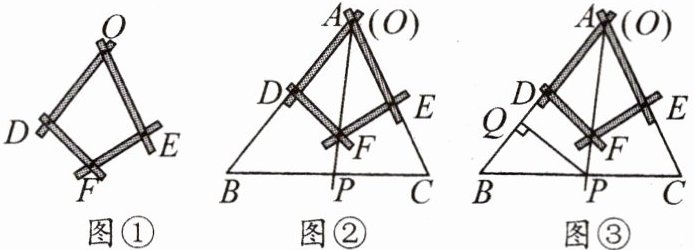
(1)如图②,将仪器放置在△ABC上,使点O与顶点A重合,点D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P.AP是∠BAC的平分线吗?请判断并说明理由;
(2)如图③,在(1)的条件下,过点P作PQ⊥AB于点Q,若PQ= 4,AC= 6,求△APC的面积。

(1)如图②,将仪器放置在△ABC上,使点O与顶点A重合,点D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P.AP是∠BAC的平分线吗?请判断并说明理由;
(2)如图③,在(1)的条件下,过点P作PQ⊥AB于点Q,若PQ= 4,AC= 6,求△APC的面积。
答案:
解:
(1)AP是∠BAC的平分线.理由如下:
在△ADF和△AEF中,
AD = AE,AF = AF,DF = EF,
∴△ADF ≌ △AEF(SSS),
∴∠DAF = ∠EAF,
∴AP平分∠BAC;
(2)过点P作PM⊥AC于点M.
∵AP平分∠BAC,PQ⊥AB,
∴PM = PQ = 4,
∴S△APC = $\frac{1}{2}$AC·PM = $\frac{1}{2}$×6×4 = 12.

解:
(1)AP是∠BAC的平分线.理由如下:
在△ADF和△AEF中,
AD = AE,AF = AF,DF = EF,
∴△ADF ≌ △AEF(SSS),
∴∠DAF = ∠EAF,
∴AP平分∠BAC;
(2)过点P作PM⊥AC于点M.
∵AP平分∠BAC,PQ⊥AB,
∴PM = PQ = 4,
∴S△APC = $\frac{1}{2}$AC·PM = $\frac{1}{2}$×6×4 = 12.

13. 如图,在Rt△ABC中,∠C= 90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,BD= DF。
(1)求证:BE= FC;
(2)若AB= 15,AF= 9,求FC的长。
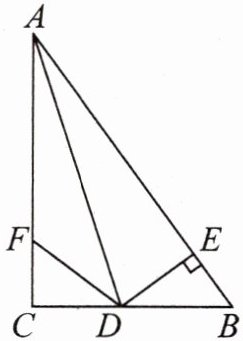
(1)求证:BE= FC;
(2)若AB= 15,AF= 9,求FC的长。

答案:
解:
(1)证明:
∵AD平分∠BAC,DE⊥AB,∠C = 90°,
∴DE = DC.
又
∵BD = DF,DE = DC,
∴Rt△BED ≌ Rt△FCD(HL),
∴BE = FC;
(2)
∵AD平分∠BAC,DE⊥AB,∠C = 90°,
∴DE = DC.又
∵AD = AD,DE = DC,
∴Rt△ADC ≌ Rt△ADE(HL),
∴AE = AC.
∵AF = 9,
∴AE = AC = AF + FC = 9 + FC.
∵AB = 15,
∴BE = AB - AE = 15 - 9 - FC = 6 - FC.
根据
(1)得BE = FC,
∴FC = 6 - FC,解得FC = 3.
(1)证明:
∵AD平分∠BAC,DE⊥AB,∠C = 90°,
∴DE = DC.
又
∵BD = DF,DE = DC,
∴Rt△BED ≌ Rt△FCD(HL),
∴BE = FC;
(2)
∵AD平分∠BAC,DE⊥AB,∠C = 90°,
∴DE = DC.又
∵AD = AD,DE = DC,
∴Rt△ADC ≌ Rt△ADE(HL),
∴AE = AC.
∵AF = 9,
∴AE = AC = AF + FC = 9 + FC.
∵AB = 15,
∴BE = AB - AE = 15 - 9 - FC = 6 - FC.
根据
(1)得BE = FC,
∴FC = 6 - FC,解得FC = 3.
14. 新情境 情境设题 如图,为了促进当地旅游发展,某地要在三条公路AB,AC,BC两两相交的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应选择的位置是△ABC三条

角平分线
的交点,这样的点一共有 4
处。
答案:
角平分线 4
查看更多完整答案,请扫码查看


