《2025年黄冈金牌之路练闯考八年级数学上册华师大版》

10. 如图,将一张长方形纸片 $ ABCD $ 沿 $ BD $ 折叠,点 $ C $ 落在点 $ C^{\prime} $ 处,$ BC^{\prime} $ 交 $ AD $ 于点 $ E $.若 $ AB = 4 $,$ BE = 5 $,则重叠部分的面积为(C)

A.$ 6 $
B.$ 8 $
C.$ 10 $
D.$ 12 $

答案： C

11. 新情境 情境设题 (驻马店期中)如图,一艘海轮位于灯塔 $ P $ 的南偏东 $ 70^{\circ} $方向的 $ M $ 处,它以 $ 40 $ 海里/时的速度向正北方向航行,$ 2 $ 小时后到达位于灯塔 $ P $ 的北偏东 $ 40^{\circ} $的 $ N $ 处,则 $ N $ 处到灯塔 $ P $ 的距离为80海里.

答案： 80

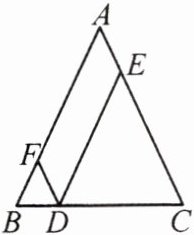
12. 如图,在 $ \triangle ABC $ 中,$ AB = AC = 10 $,过 $ BC $ 边上的一点 $ D $ 分别作 $ DE // AB $ 交 $ AC $ 于点 $ E $,$ DF // AC $ 交 $ AB $ 于点 $ F $,则四边形 $ AFDE $ 的周长为20.

答案： 20

13. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ D $ 为 $ CA $ 延长线上的一点,$ DE \perp BC $ 交 $ AB $ 于点 $ F $.
(1)求证：$ \triangle ADF $ 是等腰三角形；
(2)若 $ F $ 为 $ AB $ 的中点,求证：$ DF = 2EF $.

答案：
证明:
(1)
∵AB=AC,
∴∠B=∠C.　　又
∵DE⊥BC,
∴∠D+∠C=90°,　　∠B+∠BFE=90°.
∴∠D=∠BFE=∠AFD.
∴AD=AF,即△ADF是等腰三角形;　　
(2)过点A作AG⊥DE于点G.
∵AD=AF,AG⊥DF,
∴DF=2FG.　　又
∵AG⊥DE,BC⊥DE,
∴∠AGF=∠BEF=90°.
∵F为AB的中点,
∴AF=BF.　　又
∵∠AFG=∠BFE,
∴△AFG≌△BFE(AAS).
∴FG=FE,
∴DF=2EF.　　　　　　　　　　　　　　　　　　

14. 新课标 综合与实践 在综合实践课上,针对等腰三角形的性质“三线合一”,老师布置了这样一道课后习题：三角形一边上任意“两线合一”,能否判断该三角形是等腰三角形？
小明同学的探索过程如下：
(1)如图①,当 $ AD $ 垂直平分 $ BC $ 时,则____(______)(填写依据),即 $ \triangle ABC $ 是等腰三角形；
(2)如图②,当 $ AD \perp BC $ 于点 $ D $,$ \angle 1 = \angle 2 $ 时.
$ \because AD \perp BC $,
$ \therefore \angle ADB = \angle ADC = 90^{\circ} $.
在 $ \triangle ABD $ 和 $ \triangle ACD $ 中,$ \angle 1 = \angle 2 $,$ AD = AD $,
$ \therefore \triangle ABD \cong \triangle ACD $(____)(填简写依据).
$ \therefore AB = AC $,即 $ \triangle ABC $ 是等腰三角形；
(3)如图③,当 $ BD = CD $,$ \angle 1 = \angle 2 $ 时,显然,图中不具备判定两个三角形全等的条件,小明灵机一动,想到了老师说过的可以通过作辅助线用“倍长中线法”(或其他作辅助线的方法)来判定.请按照小明的思路判断 $ \triangle ABC $ 是否是等腰三角形.

答案：
解:
(1)AB=AC;线段垂直平分线上的点与这条线段两个端点的距离相等;　　
(2)ASA;　　
(3)△ABC是等腰三角形.　　理由如下:如图,延长AD至点E,使DE=AD,连结BE.
∵AD=ED,∠ADC=∠EDB,CD=BD,
∴△ADC≌△EDB(SAS).
∴∠E=∠2,AC=BE.　　又
∵∠1=∠2,
∴∠1=∠E,
∴AB=BE=AC,即△ABC是等腰三角形.