《2025年黄冈金牌之路练闯考八年级数学上册华师大版》

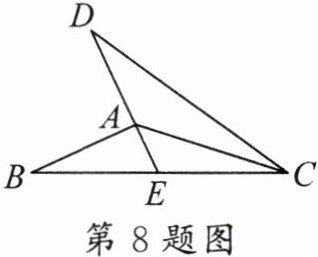
8. 如图,AC 平分∠DCB,CB = CD,DA 的延长线交 BC 于点 E,若∠EAC = 48°,则∠BAE 的度数为(A)

A.84°
B.90°
C.88°
D.96°

答案： A

9. 如图,在△ABC 中,AB = 12,BC = 15,AC = 8,AD 平分∠BAC 交 BC 于点 D,在 AB 上截取 AE = AC,则△BDE 的周长为(A)

A.19
B.20
C.18
D.17

答案： A

10. (商丘期末改)如图,在△PAB 中,∠A = ∠B,M,N,K 分别是 PA,PB,AB 上的点,且 AM = BK,BN = AK,若∠MKN = 40°,则∠A = 40°,此时∠P 的度数为100°。
]

答案： 40° 100°

11. 如图,A,F,C,D 四点在同一直线上,AF = CD,AB//DE,且 AB = DE。求证：
(1)△ABC≌△DEF；
(2)∠CBF = ∠FEC。
]

答案： 证明:
(1)
∵AB//DE,
∴∠A=∠D.
又
∵AF=CD,
∴AF+FC=CD+FC,
∴AC=DF.
又
∵AB=DE,
∴△ABC≌△DEF(SAS);
(2)
∵△ABC≌△DEF，
∴BC=EF,∠ACB=∠DFE.
又
∵FC=CF,
∴△FBC≌△CEF(SAS)，
∴∠CBF=∠FEC.

12. (周口期中)如图①,AB = 4 cm,AC⊥AB,BD⊥AB,AC = BD = 3 cm。点 P 在线段 AB 上以 1 cm/s 的速度由点 A 向点 B 运动,同时,点 Q 在线段 BD 上由点 B 向点 D 运动,它们运动的时间为 t(s)。
(1)若点 Q 的运动速度与点 P 的运动速度相等,当 t = 1 时,△ACP 与△BPQ 是否全等,请说明理由,并判断此时线段 PC 和线段 PQ 的位置关系；
(2)如图②,将图①中的“AC⊥AB,BD⊥AB”改为“∠CAB = ∠DBA”,其他条件不变。设点 Q 的运动速度为 x cm/s,是否存在实数 x,使得△ACP 与△BPQ 全等？若存在,求出相应的 x 的值；若不存在,请说明理由。

]

答案： 解:
(1)全等,PC⊥PQ.
理由:当t=1时,AP=BQ=1，
BP=AB-AP=3=AC.
又
∵∠A=∠B=90°，
∴△ACP≌△BPQ(SAS)，
∴∠ACP=∠BPQ，
∴∠APC+∠BPQ=∠APC+∠ACP=90°，
∴∠CPQ=180°-(∠APC+∠BPQ)=90°,即线段 PC 与线段 PQ 垂直；
(2)存在.理由:①若△ACP≌△BPQ，
则 AC=BP,AP=BQ，
∴{3=4-t，解得{t=1，
{t=xt， {x=1；
②若△ACP≌△BQP,则 AC=BQ,AP=BP，
∴{3=xt，解得{t=2，
{t=4-t， {x=3/2.
综上所述,存在x=1或x=3/2使得△ACP 与△BPQ 全等.