《2025年黄冈金牌之路练闯考八年级数学上册华师大版》

1. 如图,AB 与 CD 相交于点 O,OC = OD。若用“SAS”判定△AOC≌△BOD,则还需添加的一个条件是(B)

A.∠A = ∠D
B.AO = BO
C.AC = BO
D.AB = CD

答案： B

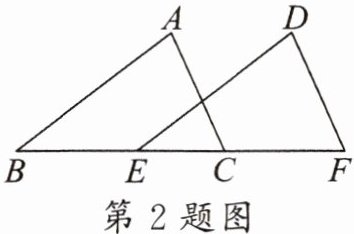
2. (济源市期末改)如图,AB = DE,∠B = ∠DEF,运用“SAS”判定△ABC≌△DEF,则需要补充的条件是BC=EF 或 BE=CF。

答案： BC=EF 或 BE=CF

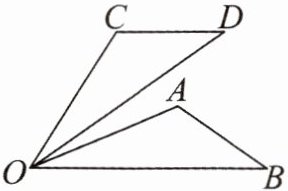
3. 如图,已知 OA = OC,OB = OD,∠AOC = ∠BOD。求证：△AOB≌△COD。
]

答案： 证明:
∵∠AOC=∠BOD，
∴∠AOC-∠AOD=∠BOD-∠AOD，
即∠COD=∠AOB.
∵OA=OC,OB=OD，
∴△AOB≌△COD(SAS).

4. 已知：如图,D、E 分别在 AB、AC 上,若 AB = AC,AD = AE,∠A = 60°,∠B = 35°,求∠BDC 的度数。
]

答案： 解:
∵AE=AD,∠A=∠A，
AB=AC，
∴△ABE≌△ACD(SAS),
∴∠C=∠B，
∵∠B=35°,
∴∠C=35°，
∵∠A=60°,
∴∠BDC=∠A+∠C=95°.

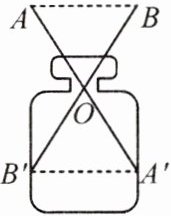
5. (教材练习变式)如图,AA',BB'表示两根长度相同的木条,若 O 是 AA',BB'的中点,经测量,AB = 9 cm,则容器的内径 A'B'的长为(B)

A.8 cm
B.9 cm
C.10 cm
D.11 cm
]

答案： B

6. 新情境 情境设题 如图,为了测量池塘两端 A,B 之间的距离,在地面上选取可以直接到达点 A 和点 B 的点 C,连结 AC,BC,再在地面上选取一点 D(可直接到达),连结 DB,DC,使 CB 平分∠ACD,AC = DC(点 A,B,C,D 在同一平面内),此时测量出线段 BD 的长便是池塘两端 A,B 之间的距离。请你说明其中的道理。(要求写出每步推理的根据)
]

答案： 解:
∵CB 平分∠ACD,(已知)
∴∠ACB=∠DCB.(角平分线的定义)
又
∵AC=DC,BC=BC,(已知)
∴△ACB≌△DCB(SAS).
∴BD=AB.(全等三角形的对应边相等)

7. 小明在学完“用 SAS 判定三角形全等”这节后,自己进行小结,做了如图分析。

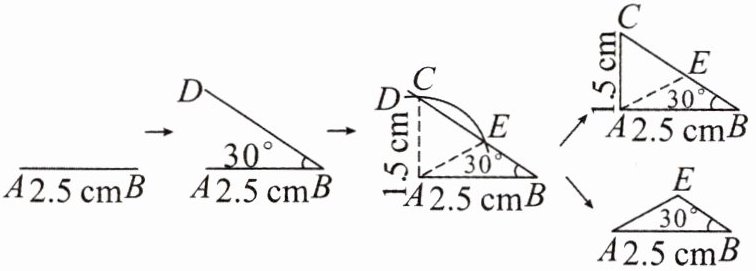
根据图中信息可知△ABC 和△ABE不全等。(填“全等”和“不全等”)；
这说明：两边和一角对应相等的三角形不一定全等。

答案： 不全等 两边和一角对应相等的三角形不一定全等