《2025年黄冈金牌之路练闯考八年级数学上册华师大版》

1. 如图,已知线段AB,观察作图痕迹,所得结论不一定成立的是(D)

A.$ AP = BP $
B.$ AO = BO $
C.$ PQ \perp AB $
D.$ \angle PAB = 30^{\circ} $

答案： D

2. 新课标 过程学习 在学完全等三角形的判定后,老师出了这样一个题：如图,已知线段BC,分别以点B,C为圆心,大于$ \frac{1}{2}BC $的长为半径画弧,两弧交于点M,N,作直线MN,交BC于点D. 求证：直线MN是线段BC的垂直平分线.

答案： 证明:由作图痕迹可知 BM=CM,BN=CN.又
∵MN=MN(已知),
∴△BMN≌△CMN(SSS),
∴∠BMD=∠CMD.
∵BM=CM,
∴BD= DC 且 MD⊥BC,即直线 MN 为线段 BC 的垂直平分线.

3. 下面关于等边三角形的说法不正确的是(C)
A.三边都相等
B.三个角都相等,并且每一个角都等于$ 60^{\circ} $
C.是轴对称图形,有6条对称轴
D.具有等腰三角形的性质

答案： C

4. 如图,$ \triangle ABC $是等边三角形,点D在AC边上,$ \angle DBC = 35^{\circ} $,则$ \angle ADB $的度数为(D)

A.$ 25^{\circ} $
B.$ 60^{\circ} $
C.$ 85^{\circ} $
D.$ 95^{\circ} $

答案： D

5. 如图,AD是等边三角形ABC的角平分线,若$ AB = 4 $,则BD = 2.

答案： 2

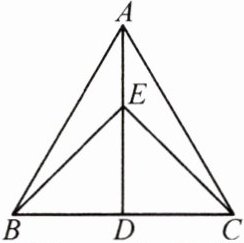
6. (禹州市期中)如图,在等边三角形ABC中,AD是BC的中线,点E在线段AD上,$ \angle EBC = 45^{\circ} $,则$ \angle ACE $的度数为(A)

A.$ 15^{\circ} $
B.$ 30^{\circ} $
C.$ 45^{\circ} $
D.$ 60^{\circ} $

答案： A

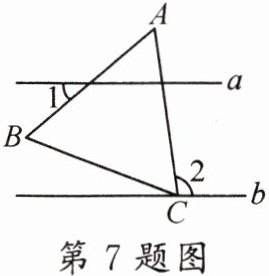
7. 如图,直线$ a // b $,等边$ \triangle ABC $的顶点C在直线b上,若$ \angle 1 = 38^{\circ} $,则$ \angle 2 $的度数为(C)

A.$ 142^{\circ} $
B.$ 128^{\circ} $
C.$ 98^{\circ} $
D.$ 92^{\circ} $

答案： C

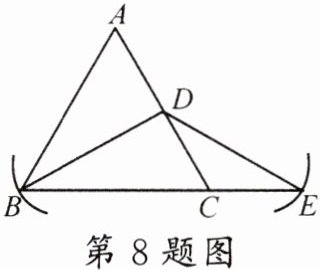
8. 如图,BD是等边三角形ABC的边AC上的中线,以点D为圆心,DB的长为半径作弧交BC的延长线于点E,若$ AB = 6 cm $,则CE的长为3cm.

答案： 3

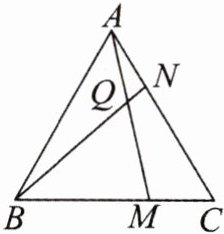
9. 如图,$ \triangle ABC $为等边三角形,M是线段BC上的任意一点,N是线段CA上任意一点,且$ BM = CN $,直线BN与AM交于点Q.
(1)求证：$ \triangle BAN \cong \triangle ACM $；
(2)求$ \angle BQM $的大小.

答案： 解:
(1)
∵△ABC 为等边三角形,
∴AB=BC=CA,∠BAC=∠BCA=60°.
∵BM=CN,
∴CM=AN,又
∵∠BAN=∠ACM,
∴△BAN≌△ACM(SAS);
(2)
∵△BAN≌△ACM,
∴∠CAM=∠ABN,
∴∠BQM = ∠ABN + ∠BAQ = ∠CAM + ∠BAQ=∠BAC=60°.

10. (洛阳期中改)如图所示,$ \triangle ABC $,$ \triangle ADE 与 \triangle EFG $都是等边三角形,D和G分别为AC和AE的中点,若$ AB = 4 $时,则图形ABCDEFG外围的周长是15.

答案： 15