第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
——教材 P13 阅读材料拓展

任务:
(1)上述材料中说明问题的方式主要体现了下列哪种数学思想______。
A.方程思想 B.数形结合思想 C.化归思想
(2)“类比思考”中,线段$OB$的长为______,$OB'$的长为______,则点$B$表示的数为______,点$B'$表示的数为______。
(3)拓展思考:通过动手操作,小敏同学把长为 5,宽为 1 的长方形进行裁剪,拼成如图④所示的大正方形。请借鉴材料中的方法在数轴上找到表示$\sqrt{5} - 1的点P$。(保留作图痕迹并标出必要线段长)
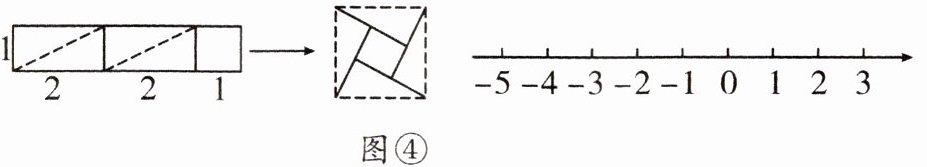

任务:
(1)上述材料中说明问题的方式主要体现了下列哪种数学思想______。
A.方程思想 B.数形结合思想 C.化归思想
(2)“类比思考”中,线段$OB$的长为______,$OB'$的长为______,则点$B$表示的数为______,点$B'$表示的数为______。
(3)拓展思考:通过动手操作,小敏同学把长为 5,宽为 1 的长方形进行裁剪,拼成如图④所示的大正方形。请借鉴材料中的方法在数轴上找到表示$\sqrt{5} - 1的点P$。(保留作图痕迹并标出必要线段长)
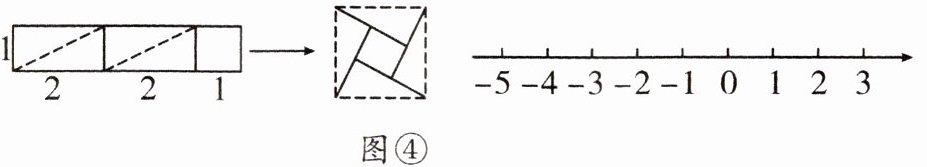
答案:
(1)B
(2)$1+\sqrt{2},\sqrt{2}-1,1+\sqrt{2},-\sqrt{2}+1$
[解析]因为正方形的对角线长为$\sqrt{2}$,所以线段OB的长为$1+\sqrt{2}$,$OB'$的长为$\sqrt{2}-1$,点B表示的数为$1+\sqrt{2}$,点$B'$表示的数为$-\sqrt{2}+1$;
(3)
因为大正方形的面积为5,所以小长方形的对角线长为$\sqrt{5}$.
小长方形的长和宽分别为2和1,以数字−1所在的点为圆心,小长方形的对角线长为半径画弧,与数轴在原点的右侧交于点P,则点P对应的数为$\sqrt{5}-1$.
(1)B
(2)$1+\sqrt{2},\sqrt{2}-1,1+\sqrt{2},-\sqrt{2}+1$
[解析]因为正方形的对角线长为$\sqrt{2}$,所以线段OB的长为$1+\sqrt{2}$,$OB'$的长为$\sqrt{2}-1$,点B表示的数为$1+\sqrt{2}$,点$B'$表示的数为$-\sqrt{2}+1$;
(3)

因为大正方形的面积为5,所以小长方形的对角线长为$\sqrt{5}$.
小长方形的长和宽分别为2和1,以数字−1所在的点为圆心,小长方形的对角线长为半径画弧,与数轴在原点的右侧交于点P,则点P对应的数为$\sqrt{5}-1$.
查看更多完整答案,请扫码查看


