第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
9. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 3$,$BC = 4$,则点$C到AB$的距离是(
A.$\frac{4}{5}$
B.$\frac{3}{5}$
C.$\frac{12}{5}$
D.$\frac{3}{4}$
C
)A.$\frac{4}{5}$
B.$\frac{3}{5}$
C.$\frac{12}{5}$
D.$\frac{3}{4}$
答案:
C
10. (河南中考)如图,在四边形$ABCD$中,$AD// BC$,$\angle D = 90^{\circ}$,$AD = 4$,$BC = 3$。分别以点$A$,$C$为圆心,大于$\frac{1}{2}AC$的长为半径作弧,两弧交于点$E$,作射线$BE交AD于点F$,交$AC于点O$。若$O是AC$的中点,则$CD$的长为(

A.$\sqrt{8}$
B.4
C.3
D.$\sqrt{10}$
A
)
A.$\sqrt{8}$
B.4
C.3
D.$\sqrt{10}$
答案:
A
11. 如图,直线$l过正方形ABCD的顶点B$,点$A$,$C到直线l$的距离分别是1和2,则正方形的边长是
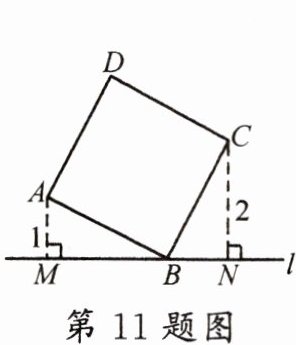
$\sqrt{5}$
。
答案:
$\sqrt{5}$
12. 如图,在四边形草坪$ABCD$中,$\angle B = \angle D = 90^{\circ}$,$AB = 20\ m$,$BC = 15\ m$,$CD = 7\ m$。求这块草坪$ABCD$的面积。


答案:
解:连结AC,
∵∠B=90°,由勾股定理知$AC^{2}=AB^{2}+BC^{2}$,

∴$AC^{2}=625$.
又
∵∠D=90°,
∴$AD^{2}+DC^{2}=AC^{2}$.
∴$AD=\sqrt{AC^{2}-CD^{2}}=24$.
∴$S_{四边形ABCD}=S_{\triangle ABC}+S_{\triangle ADC}=\frac{1}{2}AB× BC+\frac{1}{2}AD× DC=234\ m^{2}$.
解:连结AC,
∵∠B=90°,由勾股定理知$AC^{2}=AB^{2}+BC^{2}$,

∴$AC^{2}=625$.
又
∵∠D=90°,
∴$AD^{2}+DC^{2}=AC^{2}$.
∴$AD=\sqrt{AC^{2}-CD^{2}}=24$.
∴$S_{四边形ABCD}=S_{\triangle ABC}+S_{\triangle ADC}=\frac{1}{2}AB× BC+\frac{1}{2}AD× DC=234\ m^{2}$.
13. 阅读小敏的日记后完成任务。
×年×月×日 星期五 天气:晴
从勾股定理到面积关系的思考
经过《直角三角形三边的关系》一节的学习,我已经知道:如图①,分别以$Rt\triangle ABC$的三边为边向外作三个正方形,则根据勾股定理易得出这三个正方形的面积$S_{1}$,$S_{2}$,$S_{3}$之间的数量关系为______。
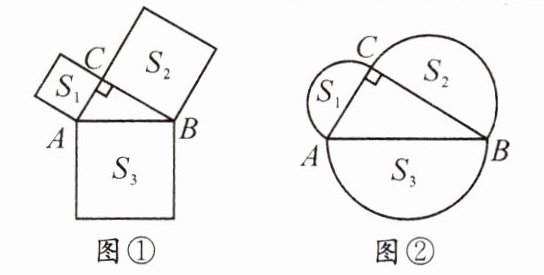
如果将正方形改成其他图形,那么这个面积之间的数量关系是否仍然成立呢?
对此,我展开了探究:如图②,分别以$Rt\triangle ABC$的三边为直径向外作三个半圆,我发现这三个半圆的面积$S_{1}$,$S_{2}$,$S_{3}$之间的数量关系?成立,理由如下:……
任务1:请直接写出图①中的$S_{1}$,$S_{2}$,$S_{3}$之间的数量关系:
任务2:“?”表示
任务3:如图③,分别以$Rt\triangle ABC$的三边为直径向上作半圆,图中的阴影部分在数学史上被称为“希波克拉底月牙”。若$AC = 4$,$BC = 6$,求阴影部分的面积。
]

×年×月×日 星期五 天气:晴
从勾股定理到面积关系的思考
经过《直角三角形三边的关系》一节的学习,我已经知道:如图①,分别以$Rt\triangle ABC$的三边为边向外作三个正方形,则根据勾股定理易得出这三个正方形的面积$S_{1}$,$S_{2}$,$S_{3}$之间的数量关系为______。

如果将正方形改成其他图形,那么这个面积之间的数量关系是否仍然成立呢?
对此,我展开了探究:如图②,分别以$Rt\triangle ABC$的三边为直径向外作三个半圆,我发现这三个半圆的面积$S_{1}$,$S_{2}$,$S_{3}$之间的数量关系?成立,理由如下:……
任务1:请直接写出图①中的$S_{1}$,$S_{2}$,$S_{3}$之间的数量关系:
$S_{3}=S_{1}+S_{2}$
;任务2:“?”表示
仍然
(填“仍然”或“不”),并说明理由;任务3:如图③,分别以$Rt\triangle ABC$的三边为直径向上作半圆,图中的阴影部分在数学史上被称为“希波克拉底月牙”。若$AC = 4$,$BC = 6$,求阴影部分的面积。
]

答案:
任务1:$S_{3}=S_{1}+S_{2}$;任务2:仍然,理由如下:在Rt△ABC中,由勾股定理,得$AC^{2}+BC^{2}=AB^{2}$.
∵$S_{1}=\frac{1}{2}\pi \left( \frac{AC}{2}\right)^{2}=\frac{\pi}{8}AC^{2}$,$S_{2}=\frac{1}{2}\pi \left( \frac{BC}{2}\right)^{2}=\frac{\pi}{8}BC^{2}$,$S_{3}=\frac{1}{2}\pi \left( \frac{AB}{2}\right)^{2}=\frac{\pi}{8}AB^{2}$,
∴$S_{1}+S_{2}=\frac{\pi}{8}(AC^{2}+BC^{2})=\frac{\pi}{8}AB^{2}=S_{3}$;任务3:同任务2可得$S_{半圆AC}+S_{半圆BC}=S_{半圆AB}$,
∴$S_{阴影部分}=S_{半圆AC}+S_{半圆BC}+S_{\triangle ABC}-S_{半圆AB}=S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}× 4× 6=12$.
∵$S_{1}=\frac{1}{2}\pi \left( \frac{AC}{2}\right)^{2}=\frac{\pi}{8}AC^{2}$,$S_{2}=\frac{1}{2}\pi \left( \frac{BC}{2}\right)^{2}=\frac{\pi}{8}BC^{2}$,$S_{3}=\frac{1}{2}\pi \left( \frac{AB}{2}\right)^{2}=\frac{\pi}{8}AB^{2}$,
∴$S_{1}+S_{2}=\frac{\pi}{8}(AC^{2}+BC^{2})=\frac{\pi}{8}AB^{2}=S_{3}$;任务3:同任务2可得$S_{半圆AC}+S_{半圆BC}=S_{半圆AB}$,
∴$S_{阴影部分}=S_{半圆AC}+S_{半圆BC}+S_{\triangle ABC}-S_{半圆AB}=S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}× 4× 6=12$.
查看更多完整答案,请扫码查看


