第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
5. 在实数范围内分解因式:
(1) $x^{4} - 9$;
(2) $x^{2} - 2\sqrt{3}x + 3$;
(3) $x^{4} - 4x^{2} + 4$。
(1) $x^{4} - 9$;
(2) $x^{2} - 2\sqrt{3}x + 3$;
(3) $x^{4} - 4x^{2} + 4$。
答案:
5.解:
(1)原式$=(x²+3)(x²-3)=(x²+3)(x-\sqrt{3})(x+\sqrt{3});(2)$原式$=(x-\sqrt{3})²;(3)$原式$=(x²-2)²=(x+\sqrt{2})²(x-\sqrt{2})².$
(1)原式$=(x²+3)(x²-3)=(x²+3)(x-\sqrt{3})(x+\sqrt{3});(2)$原式$=(x-\sqrt{3})²;(3)$原式$=(x²-2)²=(x+\sqrt{2})²(x-\sqrt{2})².$
6. 分解因式:
(1) $m^{2} - mn + mx - nx$;
(2) $x^{2} - 2x + 4y - 4y^{2}$;
(1) $m^{2} - mn + mx - nx$;
(2) $x^{2} - 2x + 4y - 4y^{2}$;
答案:
6.解:
(1)原式=(m²-mn)+(mx-nx)=m(m-n)+x(m-n)=(m-n)(m+x);
(2)原式=(x²-4y²)+(-2x+4y)=(x+2y)(x-2y)-2(x-2y)=(x-2y)(x+2y-2).
(1)原式=(m²-mn)+(mx-nx)=m(m-n)+x(m-n)=(m-n)(m+x);
(2)原式=(x²-4y²)+(-2x+4y)=(x+2y)(x-2y)-2(x-2y)=(x-2y)(x+2y-2).
微专题 二次项系数为 1 的十字相乘法
整式乘法与因式分解是相反的变形,如整式乘法 $(x + p)(x + q) = x^{2} + (p + q)x + pq$,反过来为 $x^{2} + (p + q)x + pq = (x + p)(x + q)$,恰好是因式分解.
基于上述原理,将式子 $x^{2} - x - 6$ 分解因式.如下:
$x^{2} - x - 6$
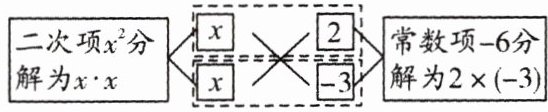
一次项: $-x = x \cdot (-3) + x \cdot 2$
① 分解二次项和常数项;② 交叉相乘验一次项: $x × 2 + x × (-3) = -x$;③ 横向写出两因式的积: $x^{2} - x - 6 = (x + 2)(x - 3)$.
根据以上信息分解因式:
- (1) $x^{2} - 3x + 2$;
- (2) $x^{2} + 7x - 18$;
- (3) $x^{2} + 2xy - 8y^{2}$。
整式乘法与因式分解是相反的变形,如整式乘法 $(x + p)(x + q) = x^{2} + (p + q)x + pq$,反过来为 $x^{2} + (p + q)x + pq = (x + p)(x + q)$,恰好是因式分解.
基于上述原理,将式子 $x^{2} - x - 6$ 分解因式.如下:
$x^{2} - x - 6$

一次项: $-x = x \cdot (-3) + x \cdot 2$
① 分解二次项和常数项;② 交叉相乘验一次项: $x × 2 + x × (-3) = -x$;③ 横向写出两因式的积: $x^{2} - x - 6 = (x + 2)(x - 3)$.
根据以上信息分解因式:
- (1) $x^{2} - 3x + 2$;
- (2) $x^{2} + 7x - 18$;
- (3) $x^{2} + 2xy - 8y^{2}$。
答案:
解:
(1)原式=(x-1)(x-2);
(2)原式=(x+9)(x-2);
(3)原式=(x+4y)(x-2y).
(1)原式=(x-1)(x-2);
(2)原式=(x+9)(x-2);
(3)原式=(x+4y)(x-2y).
查看更多完整答案,请扫码查看


