第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. (信阳月考改)如图,池塘边有两点$A$,$B$,点$C是与BA方向成直角的AC$方向上一点,测得$CB长为5m$,$AC长为3m$,则$A$,$B$两点间的距离是(
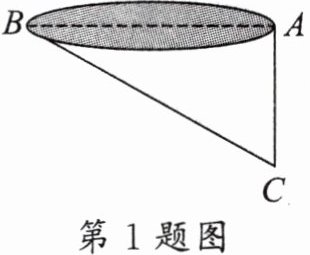
A.$2m$
B.$3m$
C.$4m$
D.$5m$
C
)
A.$2m$
B.$3m$
C.$4m$
D.$5m$
答案:
C
2. 如图,一棵大树在一次强台风中于离地面$5$米处折断倒下,树干顶部在离根部$12$米处,则这棵大树的高度为(
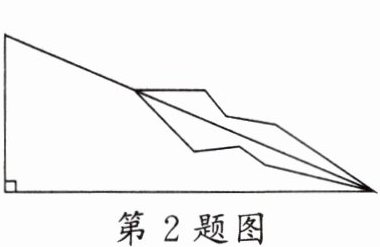
A.$13$米
B.$17$米
C.$18$米
D.$25$米
C
)
A.$13$米
B.$17$米
C.$18$米
D.$25$米
答案:
C
3. (驻马店期中)如图,学校有一块长方形花圃,有极少数人为了避开拐角走捷径,在花圃内走出了一条“路”$AB$。他们仅仅少走了几步路,却踩伤了花草。他们少走的路长为(

A.$2m$
B.$3m$
C.$3.5m$
D.$4m$
D
)
A.$2m$
B.$3m$
C.$3.5m$
D.$4m$
答案:
D
4. 如图,在笔直的公路$AB$旁有一座山,为方便运输货物现要从公路$AB上的D处开凿隧道通一条公路到C$处,已知点$C与公路上的停靠站A的距离为6km$,与公路上另一停靠站$B的距离为8km$,且$AC\perp BC$,$CD\perp AB$。公路$CD$建成后,一辆货车由$C处途经D处到达B处的总路程是多少km$?


答案:
解:
∵AC=6km,BC=8km,AC⊥BC,
∴AB=√(AC²+BC²)=10(km).
∵S△ABC=1/2AC·BC=1/2AB·DC,
∴6×8=10×CD.
∴CD=24/5(km).
∴BD=√(BC²-CD²)=32/5(km).
∴货车由C处途经D处到达B处的总路程为CD+BD=24/5+32/5=56/5(km).
∵AC=6km,BC=8km,AC⊥BC,
∴AB=√(AC²+BC²)=10(km).
∵S△ABC=1/2AC·BC=1/2AB·DC,
∴6×8=10×CD.
∴CD=24/5(km).
∴BD=√(BC²-CD²)=32/5(km).
∴货车由C处途经D处到达B处的总路程为CD+BD=24/5+32/5=56/5(km).
5. 如图,将长为$8cm$的橡皮筋放置在水平面上,固定两端$A和B$,然后把中点$C垂直向上拉升3cm至点D$,则橡皮筋被拉长了(
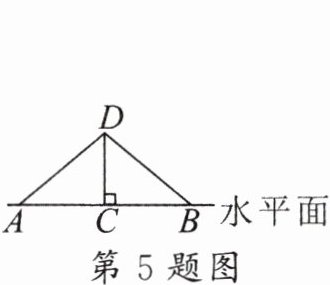
A.$2cm$
B.$3cm$
C.$4cm$
D.$6cm$
A
)
A.$2cm$
B.$3cm$
C.$4cm$
D.$6cm$
答案:
A
6. (教材练习变式)如图所示,有一“工”字形的机器零件,它是轴对称图形,图中所有的角都是直角,那么$A$,$B$两点之间的距离为(图中数据单位:$cm$)(
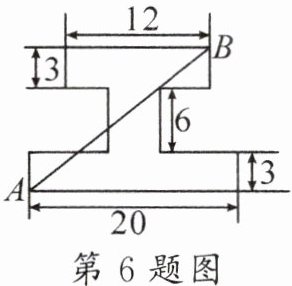
A.$8cm$
B.$12cm$
C.$16cm$
D.$20cm$
D
)
A.$8cm$
B.$12cm$
C.$16cm$
D.$20cm$
答案:
D
7. 如图,有两棵树相距$8m$,一棵树高$12m$,另一棵树高$6m$,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞

10
$m$。
答案:
10
8.思想方法 方程思想 如图,小明想测量学校旗杆$AC$的长,他采用如下的方法:先将旗杆上的绳子接长一些,让它垂到地面还多$1$米,然后将绳子下端拉直($AB$),使它刚好接触地面,测得绳下端离旗杆底部的距离为$BC = 5$米,你能帮小明计算一下吗?


答案:
解:由题意知AB=AC+1,BC=5米,AC⊥BC,则由勾股定理,得AC=√(AB²-5²)=√((AC+1)²-25),解得AC=12,答:旗杆AC的长为12米.
查看更多完整答案,请扫码查看


