《2025年黄冈金牌之路练闯考八年级数学上册华师大版》

10. 下面说法中正确的是(B)
A.“同位角相等”的题设是“两个角相等”
B.“相等的角是对顶角”是假命题.
C.如果 $ab = 0$,那么 $a + b = 0$ 是真命题
D.“任何偶数都是 4 的倍数”是真命题

答案： B

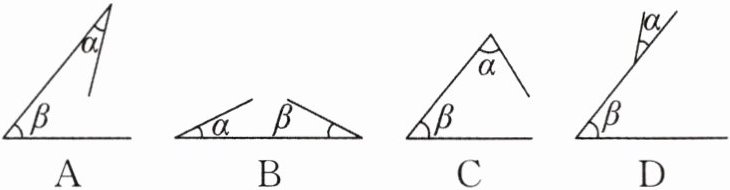
11. 能说明“锐角 $\alpha$,锐角 $\beta$ 的和是锐角”是假命题的例证图是(C)
]

答案： C

12.(枫杨外国语学校期末)下列命题：①数轴上的点和实数是一一对应的；②若点 $Q(-2,-1)$,则点 $Q$ 关于 $x$ 轴对称的点的坐标为 $(2,-1)$；③三角形的一个外角大于任何一个与其不相邻的内角；④在 $Rt\triangle ABC$ 中,已知两边长分别是 3 和 4,则第三条边长为 5.其中真命题为①③.(填序号)

答案： ①③

13. 新考向 结论开放 对于同一平面内的三条直线 $a$,$b$,$c$,给出下列五个论断：①$a// b$；②$b// c$；③$a\perp b$；④$a// c$；⑤$a\perp c$.以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题：如果a//b,b//c.那么a//c(答案不唯一).

答案： 如果a//b,b//c.那么a//c(答案不唯一)

14. 判断下列语句是不是命题,如果是命题,是真命题还是假命题？若是假命题,请举出反例.
(1)两直线相交有几个交点？
(2)同角或等角的补角相等；
(3)如果 $a + b = 0$,那么 $a = 0$,$b = 0$.

答案： 解:
(1)两直线相交有几个交点？不是命题；
(2)同角或等角的补角相等;是命题,是真命题；
(3)如果a+b=0,那么a=0,b=0;是命题,是假命题,例如:a=2,b=-2.

15.(漯河市校级期中)已知 $\angle ABC$ 和 $\angle DEF$,一个角的两边与另一个角的两边分别平行.
【探究问题】
(1)如图①,$AB// EF$,$BC// ED$,$\angle 1$ 与 $\angle 2$ 的关系是______.
推理说明：______；
(2)如图②,$AB// EF$,$BC// DE$,则 $\angle 1$ 与 $\angle 2$ 的关系是______.
推理说明：______；
【归纳总结】
(3)经过推理,你能得到的一个真命题是______；
【拓展延伸】
(4)已知 $\angle ABC$ 和 $\angle DEF$,一个角的两边与另一个角的两边互相垂直.且 $\angle DEF$ 比 $\angle ABC$ 的 2 倍少 $30^{\circ}$,请直接写出这两个角的度数.

答案：
解:
(1)∠1=∠2 根据平行线的性质易得∠1=∠3,∠2=∠3,则∠1=∠2
(2)∠1+∠2=180° 根据平行线的性质易得∠1=∠3,∠2+∠3=180°,所以∠1+∠2=180°
(3)如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补
(4)当∠DEF与∠ABC如答图①所示时,∠ABC=70°,∠DEF=110°；当∠DEF与∠ABC如答图②所示时,∠ABC=30°,∠DEF=30°.