第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
9. 下列命题的逆命题是假命题的是(
A.两直线平行,同位角相等
B.等边三角形的三个内角都相等
C.两个全等直角三角形的对应角相等
D.直角三角形的两个锐角互余
C
)A.两直线平行,同位角相等
B.等边三角形的三个内角都相等
C.两个全等直角三角形的对应角相等
D.直角三角形的两个锐角互余
答案:
C
10. 判断下列命题:
①等腰三角形是轴对称图形;②若 $ a > 1 $ 且 $ b > 1 $,则 $ a + b > 2 $;③全等三角形对应角相等;④直角三角形的两锐角互余。
其中逆命题正确的有(
A.1 个
B.2 个
C.3 个
D.0 个
①等腰三角形是轴对称图形;②若 $ a > 1 $ 且 $ b > 1 $,则 $ a + b > 2 $;③全等三角形对应角相等;④直角三角形的两锐角互余。
其中逆命题正确的有(
A
)A.1 个
B.2 个
C.3 个
D.0 个
答案:
A
11. 命题“两直线平行,内错角相等”的条件是
两直线平行
,结论是内错角相等
,这个命题的逆命题的条件是内错角相等
,结论是两直线平行
。
答案:
两直线平行 内错角相等 内错角相等 两直线平行
12. 定理“等边对等角”的逆定理是
等角对等边
。
答案:
等角对等边
13. 如果 $ a = 0 $ 且 $ b = 0 $,那么 $ a^{2} + b^{2} = 0 $ 的逆命题是
真命题
。(填“真命题”或“假命题”)
答案:
真命题
14. 举反例说明命题“一个锐角与一个钝角的和是 $ 180^{\circ} $”是假命题,举反例如下:
20°和100°
。
答案:
20°和100°
15. 已知命题“若 $ a > b $,则 $ a^{2} > b^{2} $”。
(1)此命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出一个反例;
(2)写出此命题的逆命题,并判断逆命题的真假,若是真命题,请给予证明;若是假命题,请举出一个反例。
(1)此命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出一个反例;
(2)写出此命题的逆命题,并判断逆命题的真假,若是真命题,请给予证明;若是假命题,请举出一个反例。
答案:
解:
(1)此命题是假命题.反例:a=2,b=-3,有a>b,但a²<b²;
(2)逆命题:若a²>b²,则a>b.此命题为假命题.反例:a=-2,b=-1,有a²>b²,但a<b.
(1)此命题是假命题.反例:a=2,b=-3,有a>b,但a²<b²;
(2)逆命题:若a²>b²,则a>b.此命题为假命题.反例:a=-2,b=-1,有a²>b²,但a<b.
16. 判断下列命题的真假,若是真命题,请给予证明;若是假命题,请举出一个反例。
(1)若 $ \sqrt{a^{2}} = 3 $,则 $ a = 3 $;
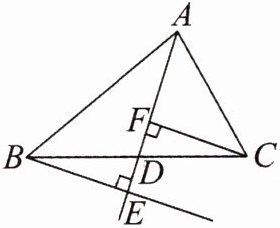
(2)如图,已知在 $ \triangle ABC $ 中,$ BE \perp AD $,$ CF \perp AD $,垂足分别为 $ E $,$ F $,且 $ BE = CF $,则 $ AD $ 是 $ \triangle ABC $ 的中线。
(1)若 $ \sqrt{a^{2}} = 3 $,则 $ a = 3 $;
(2)如图,已知在 $ \triangle ABC $ 中,$ BE \perp AD $,$ CF \perp AD $,垂足分别为 $ E $,$ F $,且 $ BE = CF $,则 $ AD $ 是 $ \triangle ABC $ 的中线。

答案:
解:
(1)是假命题,当a=-3时,$\sqrt{a^2}=3$,但a≠3,所以命题
(1)是假命题;
(2)是真命题.证明:
∵BE⊥AD,CF⊥AD,
∴∠DFC=∠DEB=90°.在△BED和△CFD中,
∵∠BDE=∠CDF,∠DEB=∠DFC,BE=CF,
∴△BED≌△CFD(AAS),
∴BD=CD,
∴AD是△ABC的中线,即命题
(2)是真命题.
(1)是假命题,当a=-3时,$\sqrt{a^2}=3$,但a≠3,所以命题
(1)是假命题;
(2)是真命题.证明:
∵BE⊥AD,CF⊥AD,
∴∠DFC=∠DEB=90°.在△BED和△CFD中,
∵∠BDE=∠CDF,∠DEB=∠DFC,BE=CF,
∴△BED≌△CFD(AAS),
∴BD=CD,
∴AD是△ABC的中线,即命题
(2)是真命题.
17. 如图,点 $ D $,$ E $ 在 $ \triangle ABC $ 的边 $ BC $ 上,连结 $ AD $,$ AE $。下面有三个等式:① $ AB = AC $;② $ AD = AE $;③ $ BD = CE $。以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成以下三个命题:命题I“如果①②成立,那么③成立”;命题II“如果①③成立,那么②成立”;命题III“如果②③成立,那么①成立”。
(1)以上三个命题是真命题的为(直接作答)
(2)请选择一个真命题进行证明(先写出所选命题,然后证明)。
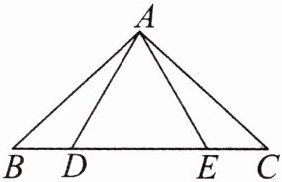
(1)以上三个命题是真命题的为(直接作答)
Ⅰ,Ⅱ,Ⅲ
;(2)请选择一个真命题进行证明(先写出所选命题,然后证明)。

答案:
解:
(1)Ⅰ,Ⅱ,Ⅲ
(2)选择命题Ⅱ“如果①③成立,那么②成立”.证明:
∵AB=AC,
∴∠B=∠C.在△ABD和△ACE中,
∵AB=AC,∠B=∠C,BD=CE,
∴△ABD≌△ACE(SAS),
∴AD=AE.
(1)Ⅰ,Ⅱ,Ⅲ
(2)选择命题Ⅱ“如果①③成立,那么②成立”.证明:
∵AB=AC,
∴∠B=∠C.在△ABD和△ACE中,
∵AB=AC,∠B=∠C,BD=CE,
∴△ABD≌△ACE(SAS),
∴AD=AE.
查看更多完整答案,请扫码查看


