《2025年黄冈金牌之路练闯考八年级数学上册华师大版》

1. 新课标 过程学习 $6x^{3}\cdot 3x^{2}= (6×$3$)\cdot$($x^{3} \cdot x^{2}$)=$18x^{5}$.

答案： 3 $x^{3} \cdot x^{2}$ $18x^{5}$

2. (常德中考)计算$-x^{4}\cdot 4x^{3}$的结果是 (C)
A.$-x$
B.$-4x$
C.$-4x^{7}$
D.$-x^{11}$

答案： C

3. 计算：(1)$3a^{2}\cdot (-2ab^{3})=$$-6a^{3}b^{4}$；
(2)$(-5a^{4})\cdot (-6ab^{3})=$$30a^{5}b^{3}$.
【启思】注意运算符号,同时不要漏乘字母因式.

答案：
(1)$-6a^{3}b^{4}$
(2)$30a^{5}b^{3}$

4. 计算：
(1)$2x^{2}y\cdot (-4xy^{3}z)$；
(2)$5a^{2}\cdot (3a^{3})^{2}$.

答案： 解:
(1)原式$=-8x^{3}y^{4}z$;
(2)原式$=5a^{2} \cdot 9a^{6}=45a^{8}$.

5. 长方形的长为$3x^{2}y$,宽为$2xy^{3}$,则它的面积为 (C)
A.$5x^{3}y^{4}$
B.$6x^{2}y^{3}$
C.$6x^{3}y^{4}$
D.$\frac{3}{2}xy^{2}$

答案： C

6. 一种电子计算机每秒可以做$6×10^{8}$次运算,它工作$8×10^{2}$秒可做$4.8× 10^{11}$次运算.

答案： $4.8× 10^{11}$

7. (洛阳偃师区期中)计算$2x\cdot (-3xy)^{2}\cdot (-x^{2}y)^{3}$的结果是 (C)
A.$18x^{8}y^{5}$
B.$6x^{9}y^{5}$
C.$-18x^{9}y^{5}$
D.$-6x^{4}y^{5}$

答案： C

8. 如果单项式$-3x^{4a - b}y^{2}与\frac{1}{3}x^{3}y^{a + b}$是同类项,那么这两个单项式的积是 (A)
A.$-x^{6}y^{4}$
B.$x^{6}y^{4}$
C.$-3x^{3}y^{2}$
D.$-\frac{8}{3}x^{3}y^{2}$

答案： A

9. (河南省实验中学月考)设$(x^{m - 1}y^{n + 2})\cdot (x^{5m}y^{2}) = x^{5}y^{7}$,则$(-\frac{1}{2}m)^{n}$的值为$-\frac{1}{8}$.

答案： $-\frac{1}{8}$

10. 计算：(1)$-2xy\cdot (-\frac{1}{2}x^{2}y^{3}z)=$$x^{3}y^{4}z$；
(2)$(-3x)\cdot \frac{2}{3}xy^{2}\cdot 6y=$$-12x^{2}y^{3}$.

答案：
(1)$x^{3}y^{4}z$
(2)$-12x^{2}y^{3}$

11. 先化简,再求值：
$(-2a^{2}b^{3})\cdot (-ab^{2})^{2} + (-\frac{1}{2}a^{2}b^{3})^{2}\cdot 4b$,其中$a = 2$,$b = 1$.

答案： 解:原式$=-2a^{2}b^{3} \cdot a^{2}b^{4}+\frac{1}{4}a^{4}b^{3} \cdot 4b=-2a^{4}b^{7}+a^{4}b^{7}=-a^{4}b^{7}$,当$a=2,b=1$时,原式$=-2^{4}× 1=-16$.

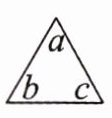
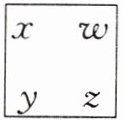
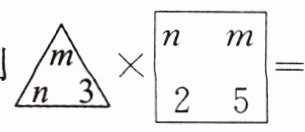
12. “三角”表示$3abc$,“方框”表示$-4x^{y}w^{z}$,则×= $-36m^{6}n^{3}$.

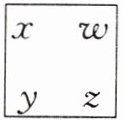
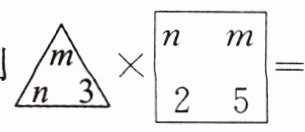
答案： $-36m^{6}n^{3}$