第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. (郑州模拟)下列运算正确的是 (
A.$x^{3}\cdot x^{3}= x^{9}$
B.$x^{8}÷ x^{4}= x^{2}$
C.$(ab^{3})^{2}= ab^{6}$
D.$(2x)^{3}= 8x^{3}$
D
)A.$x^{3}\cdot x^{3}= x^{9}$
B.$x^{8}÷ x^{4}= x^{2}$
C.$(ab^{3})^{2}= ab^{6}$
D.$(2x)^{3}= 8x^{3}$
答案:
D
2. 计算$(-\frac {1}{2}xy^{2})^{3}= $
$-\frac{1}{8}x^{3}y^{6}$
。
答案:
$-\frac{1}{8}x^{3}y^{6}$
3. 已知$a^{m}= 4,a^{n}= \frac {1}{2}$,则$a^{2m - 2n}= $
64
。
答案:
64
4. 已知$3^{m}\cdot 9^{m}\cdot 27^{m}\cdot 81^{m}= 3^{30}$,求$m$的值.
答案:
解:因为$3^{m}\cdot 2^{2m}\cdot 3^{3m}\cdot 3^{4m}=3^{10m}=3^{30}$,所以10m=30,所以m=3.
5. 计算$(x - 1)(2x + 3)$的结果是 (
A.$2x^{2}+x - 3$
B.$2x^{2}-x - 3$
C.$2x - x + 3$
D.$x^{2}-2x - 3$
A
)A.$2x^{2}+x - 3$
B.$2x^{2}-x - 3$
C.$2x - x + 3$
D.$x^{2}-2x - 3$
答案:
A
6. 若关于$x的多项式(2x - m)与(3x + 5)$的乘积中,一次项系数为$25$,则$m$的值 (
A.$5$
B.$-5$
C.$3$
D.$-3$
B
)A.$5$
B.$-5$
C.$3$
D.$-3$
答案:
B
7. 如图,若用两种方法表示图中阴影部分的面积,则可以得到的代数恒等式是 (
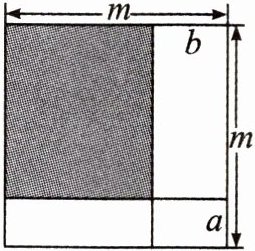
A.$(m + a)(m - b)= m^{2}+(a - b)m - ab$
B.$(m - a)(m + b)= m^{2}+(b - a)m - ab$
C.$(m - a)(m - b)= m^{2}-(a - b)m + ab$
D.$(m - a)(m - b)= m^{2}-(a + b)m + ab$
D
)
A.$(m + a)(m - b)= m^{2}+(a - b)m - ab$
B.$(m - a)(m + b)= m^{2}+(b - a)m - ab$
C.$(m - a)(m - b)= m^{2}-(a - b)m + ab$
D.$(m - a)(m - b)= m^{2}-(a + b)m + ab$
答案:
D
8. 先化简,再求值:$(a - 2)(3a + 1)-3a(a - 1)$,其中$a= -1$.
答案:
解:原式=-2a-2,当a=-1时,原式=0.
9. (南阳校级期中)下列计算正确的是 (
A.$(x + y)^{2}= x^{2}+y^{2}$
B.$(x - y)^{2}= x^{2}-2xy - y^{2}$
C.$(x + 1)(x - 1)= x^{2}-1$
D.$(x - 1)^{2}= x^{2}-1$
C
)A.$(x + y)^{2}= x^{2}+y^{2}$
B.$(x - y)^{2}= x^{2}-2xy - y^{2}$
C.$(x + 1)(x - 1)= x^{2}-1$
D.$(x - 1)^{2}= x^{2}-1$
答案:
C
10. 定义$\begin{vmatrix}a&b\\c&d\end{vmatrix} $为二阶行列式,规定它的运算法则为$\begin{vmatrix}a&b\\c&d\end{vmatrix} = ad - bc$,那么当$x = 1$时,二阶行列式$\begin{vmatrix}x + 1&1\\0&x - 1\end{vmatrix} $的值为
0
。
答案:
0
11. 先化简,再求值:
$(x + y)^{2}+(y - x)(-y - x)$,其中$\vert x-\frac{1}{2}\vert+(y+\frac{1}{3})^{2}= 0$.
$(x + y)^{2}+(y - x)(-y - x)$,其中$\vert x-\frac{1}{2}\vert+(y+\frac{1}{3})^{2}= 0$.
答案:
解:原式=$x^{2}+2xy+y^{2}+x^{2}-y^{2}=2x^{2}+2xy$.又因为$|x-\frac{1}{2}|+(y+\frac{1}{3})^{2}=0$,所以$x=\frac{1}{2},y=-\frac{1}{3}$.所以原式=$2× (\frac{1}{2})^{2}+2× \frac{1}{2}× (-\frac{1}{3})=\frac{1}{2}-\frac{1}{3}=\frac{1}{6}$.
12. (新郑市月考)【教材例题变式】
利用乘法公式计算下列各题:
(1)$2002^{2}$;
(2)$2024×2026 - 2025^{2}$.
利用乘法公式计算下列各题:
(1)$2002^{2}$;
(2)$2024×2026 - 2025^{2}$.
答案:
解:
(1)原式=$(2000+2)^{2}$=$2000^{2}+2× 2000× 2+2^{2}$=4000000+8000+4=4008004;
(2)原式=$(2025-1)× (2025+1)-2025^{2}$=$2025^{2}-1-2025^{2}$=-1.
(1)原式=$(2000+2)^{2}$=$2000^{2}+2× 2000× 2+2^{2}$=4000000+8000+4=4008004;
(2)原式=$(2025-1)× (2025+1)-2025^{2}$=$2025^{2}-1-2025^{2}$=-1.
查看更多完整答案,请扫码查看


