第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
9. (驻马店三模)如图所示,在等腰$\triangle ABC$中,$AB = AC$,$BD为AC$边上的高线,$AE // BD$,且$AE交CB的延长线于点E$。若$\angle BAC = 70^{\circ}$,则$\angle AEC$的度数为(

A.$30^{\circ}$
B.$20^{\circ}$
C.$35^{\circ}$
D.$25^{\circ}$
C
)
A.$30^{\circ}$
B.$20^{\circ}$
C.$35^{\circ}$
D.$25^{\circ}$
答案:
C
10. (郑州一模)如图,在等腰$\triangle ABC$中,$AC = BC$,$D是AB$边上的中点,$DE // AC$,交$BC于点E$。若$\angle A = 40^{\circ}$,则$\angle CDE$的度数是(
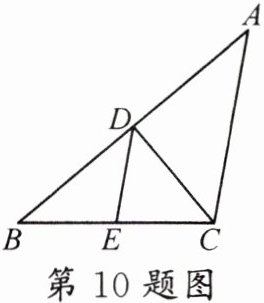
A.$40^{\circ}$
B.$35^{\circ}$
C.$50^{\circ}$
D.$45^{\circ}$
C
)
A.$40^{\circ}$
B.$35^{\circ}$
C.$50^{\circ}$
D.$45^{\circ}$
答案:
C
11. 新情境 生产生活 如图,一建筑钢架$\angle AOB = 10^{\circ}$,为使钢架更加稳固,需在内部添加一些钢管$CD$,$DE$,$EF$,$FG$,$GH$,…$$,若添加的钢管都与$OC$等长,则最多能添加这样的钢管

8
根。
答案:
8
12. 思想方法 方程思想 (教材例题变式)如图,在$\triangle ABC$中,点$D在BC$上,若$AD = BD$,$AB = AC = CD$,求$\angle BAC$的度数。


答案:
解:
∵AD=BD,
∴∠B=∠BAD.
∵AB=AC=CD,
∴∠B=∠C,∠ADC=∠CAD.
设∠B=∠BAD=∠C=x°,则∠CAD=
∠ADC=∠B+∠BAD=2x°.
在△ACD中,∠ADC+∠CAD+∠C=180°,
即2x+2x+x=180,解得x=36.
∴∠BAC=∠BAD+∠CAD=3x°=108°.
∵AD=BD,
∴∠B=∠BAD.
∵AB=AC=CD,
∴∠B=∠C,∠ADC=∠CAD.
设∠B=∠BAD=∠C=x°,则∠CAD=
∠ADC=∠B+∠BAD=2x°.
在△ACD中,∠ADC+∠CAD+∠C=180°,
即2x+2x+x=180,解得x=36.
∴∠BAC=∠BAD+∠CAD=3x°=108°.
13. 如图,在$\triangle ABC$中,$AB = AC$,点$D$,$E$,$F分别在边BC$,$AB$,$AC$上,且$BD = CF$,$BE = CD$,$G是EF$的中点,求证:$DG \perp EF$。


答案:
证明:连结DE,DF.
∵AB=AC,
∴∠B=∠C.

又
∵BD=CF,BE=CD,
∴△BDE≌△CFD(SAS).
∴DE=FD.
又
∵G是EF的中点,
∴DG⊥EF.
证明:连结DE,DF.
∵AB=AC,
∴∠B=∠C.

又
∵BD=CF,BE=CD,
∴△BDE≌△CFD(SAS).
∴DE=FD.
又
∵G是EF的中点,
∴DG⊥EF.
14. 思想方法 类比思想 在$\triangle ABC$中,$AB = AC$。
(1) 如图①,$AD是BC$边上的高,且$AD = AE$,
①若$\angle BAD = 30^{\circ}$,则$\angle EDC = $
②若$\angle BAD = 40^{\circ}$,则$\angle EDC = $
思考:$\angle BAD与\angle EDC$之间的数量关系为
(2) 如图②,$AD不是BC$边上的高,但$AD = AE$,(1)中的结论还成立吗?请说明理由。
]
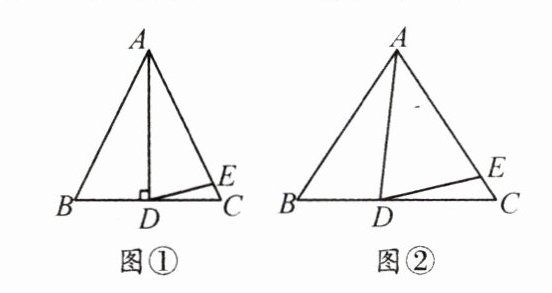
(1) 如图①,$AD是BC$边上的高,且$AD = AE$,
①若$\angle BAD = 30^{\circ}$,则$\angle EDC = $
15°
;②若$\angle BAD = 40^{\circ}$,则$\angle EDC = $
20°
。思考:$\angle BAD与\angle EDC$之间的数量关系为
∠BAD=2∠EDC
,请说明理由;(2) 如图②,$AD不是BC$边上的高,但$AD = AE$,(1)中的结论还成立吗?请说明理由。
]

答案:
解:
(1)①15° ②20°
思考:∠BAD=2∠EDC 理由如下:
∵AB=AC,AD是BC边上的高,
∴AD⊥BC,∠CAD=∠BAD.
∴∠C=90°−∠CAD.
又
∵AD=AE,
∴∠AED=$\frac{1}{2}(180^{\circ}-\angle CAD)=90^{\circ}-\frac{1}{2}\angle CAD$.
∴∠EDC=∠AED−∠C=90°-$\frac{1}{2}\angle CAD$-(90°−∠CAD)=$\frac{1}{2}\angle CAD=\frac{1}{2}\angle BAD$.
∴∠BAD=2∠EDC;
(2)成立.理由如下:
∵AD=AE,
∴∠ADE=∠AED,
∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=(∠EDC+∠C)+∠EDC=2∠EDC+∠C.
又
∵AB=AC,
∴∠B=∠C,
∴∠BAD=2∠EDC.
(1)①15° ②20°
思考:∠BAD=2∠EDC 理由如下:
∵AB=AC,AD是BC边上的高,
∴AD⊥BC,∠CAD=∠BAD.
∴∠C=90°−∠CAD.
又
∵AD=AE,
∴∠AED=$\frac{1}{2}(180^{\circ}-\angle CAD)=90^{\circ}-\frac{1}{2}\angle CAD$.
∴∠EDC=∠AED−∠C=90°-$\frac{1}{2}\angle CAD$-(90°−∠CAD)=$\frac{1}{2}\angle CAD=\frac{1}{2}\angle BAD$.
∴∠BAD=2∠EDC;
(2)成立.理由如下:
∵AD=AE,
∴∠ADE=∠AED,
∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=(∠EDC+∠C)+∠EDC=2∠EDC+∠C.
又
∵AB=AC,
∴∠B=∠C,
∴∠BAD=2∠EDC.
查看更多完整答案,请扫码查看


