第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 下列实数是无理数的是(
A.$\sqrt{11}$
B.$\sqrt{9}$
C.$\frac{1}{6}$
D.$-2$
A
)A.$\sqrt{11}$
B.$\sqrt{9}$
C.$\frac{1}{6}$
D.$-2$
答案:
A
2. 下列语句中正确的是(
A.带根号的数都是无理数
B.不带根号的数一定是有理数
C.无理数是无限不循环小数
D.无限小数是无理数
C
)A.带根号的数都是无理数
B.不带根号的数一定是有理数
C.无理数是无限不循环小数
D.无限小数是无理数
答案:
C
3. (教材习题变式) 实数 $\pi, \frac{22}{7},-\sqrt{2}, \sqrt{9}, 3.14$, $0.61414,0.2020020002…$ (每相邻两个 2 之间 0 的个数逐次加 1) 中, 无理数的个数为(
A.1 个
B.2 个
C.3 个
D.4 个
C
)A.1 个
B.2 个
C.3 个
D.4 个
答案:
C
4. 判断下列语句是否正确. (正确的画“√”, 不正确的画“×”)
(1) 无限小数都是无理数(
(2) $\pi$ 是无理数, 故无理数也可能是有限小数(
(3) 无限不循环的小数是无理数(
(4) 分数不是有理数(
(1) 无限小数都是无理数(
×
)(2) $\pi$ 是无理数, 故无理数也可能是有限小数(
×
)(3) 无限不循环的小数是无理数(
√
)(4) 分数不是有理数(
×
)
答案:
(1)×
(2)×
(3)√
(4)×
(1)×
(2)×
(3)√
(4)×
5. 下列说法正确的是(
A.实数可分为正实数和负实数
B.无理数可分为正无理数和负无理数
C.实数可分为有理数, 0, 无理数
D.无限小数是无理数
B
)A.实数可分为正实数和负实数
B.无理数可分为正无理数和负无理数
C.实数可分为有理数, 0, 无理数
D.无限小数是无理数
答案:
B
6. 下列说法错误的是(
A.$\pi$ 是实数
B.$\sqrt{2}$ 是无理数
C.$\sqrt[3]{8}$ 是有理数
D.$\frac{\sqrt{2}}{2}$ 是分数
D
)A.$\pi$ 是实数
B.$\sqrt{2}$ 是无理数
C.$\sqrt[3]{8}$ 是有理数
D.$\frac{\sqrt{2}}{2}$ 是分数
答案:
D
7. 把下列各数填在相应的表示集合的横线上 (填序号):
①$-2$, ②$\pi$, ③$-\frac{1}{3}$, ④$-|-3|$, ⑤$\frac{22}{7}$, ⑥$-0.3$, ⑦$-\sqrt{4}$, ⑧$\sqrt{5}$, ⑨$0$, ⑩$1.1010010001…$ (每两个 1 之间依次多一个 0).
正数:
整数:
分数:
非负有理数:
无理数:
负实数:
①$-2$, ②$\pi$, ③$-\frac{1}{3}$, ④$-|-3|$, ⑤$\frac{22}{7}$, ⑥$-0.3$, ⑦$-\sqrt{4}$, ⑧$\sqrt{5}$, ⑨$0$, ⑩$1.1010010001…$ (每两个 1 之间依次多一个 0).
正数:
②⑤⑧⑩
;整数:
①④⑦⑨
;分数:
③⑤⑥
;非负有理数:
⑤⑨
;无理数:
②⑧⑩
;负实数:
①③④⑥⑦
.
答案:
正数: ②⑤⑧⑩;整数: ①④⑦⑨;分数: ③⑤⑥;非负有理数: ⑤⑨;无理数: ②⑧⑩;负实数: ①③④⑥⑦
8. (南召县期中) 与数轴上的点一一对应的数是(
A.分数或整数
B.无理数
C.有理数
D.有理数和无理数
【启思】有理数和无理数统称为实数, 实数与数轴上的点一一对应.
D
)A.分数或整数
B.无理数
C.有理数
D.有理数和无理数
【启思】有理数和无理数统称为实数, 实数与数轴上的点一一对应.
答案:
D
9. 新情境 创新设题 如图, 面积为 5 的正方形 $ABCD$ 的顶点 $A$ 在数轴上, 且表示的数为 $-1$, 若点 $E$ 在数轴上 (点 $E$ 在点 $A$ 的右侧), 且 $AB = AE$, 则点 $E$ 所表示的数为(
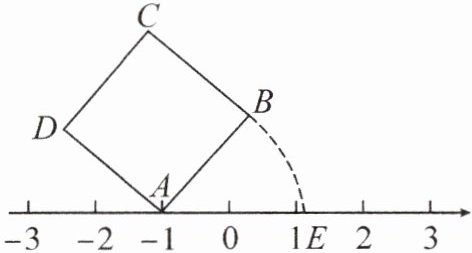
A.$\sqrt{5}$
B.$\sqrt{5}-1$
C.$\sqrt{5}+1$
D.$\sqrt{5}-2$
B
)
A.$\sqrt{5}$
B.$\sqrt{5}-1$
C.$\sqrt{5}+1$
D.$\sqrt{5}-2$
答案:
B
10. 一个实数在数轴上对应的点在负半轴上, 且到原点距离等于 $\sqrt{5}$, 则这个数为
$-\sqrt{5}$
.
答案:
$-\sqrt{5}$
11. 思想方法 数形结合 在如图所示的数轴上, 点 $B$ 与点 $C$ 关于点 $A$ 对称, $A, B$ 两点表示的实数分别是 $\sqrt{3}$ 和 $-1$, 则线段 $AC$ 的长度为


$\sqrt{3}+1$
.

答案:
$\sqrt{3}+1$
查看更多完整答案,请扫码查看


