《2025年黄冈金牌之路练闯考八年级数学上册华师大版》

1. 命题“$a$是无理数”的反面是(C)
A.$a$是正数
B.$a$是负数
C.$a$是有理数
D.$a是0$

答案： C

2. 语句“$a$,$b中至少有一个数大于0$”的反面描述是a,b均小于等于0。

答案： a,b均小于等于0

3. 用反证法证明“若$a\perp c$,$b\perp c$,则$a// b$”时,应假设(D)
A.$a不垂直于c$
B.$a$,$b都不垂直于c$
C.$a\perp b$
D.$a与b$相交

答案： D

4. “已知：在$\triangle ABC$中,$AB = AC$,求证：$\angle B\lt90^{\circ}$”。下面写出了用于证明这个命题过程中的四个推理步骤：
①所以$\angle A+\angle B+\angle C\gt180^{\circ}$,这与三角形内角和定理相矛盾；
②所以$\angle B\lt90^{\circ}$；
③假设$\angle B\geq90^{\circ}$；
④那么,由$AB = AC$,得$\angle B= \angle C\geq90^{\circ}$,即$\angle B+\angle C\geq180^{\circ}$。
这四个步骤正确的顺序应该是(C)
A.①②③④
B.③④②①
C.③④①②
D.④③①②

答案： C

5. 用反证法证明：两直线平行,同旁内角互补。
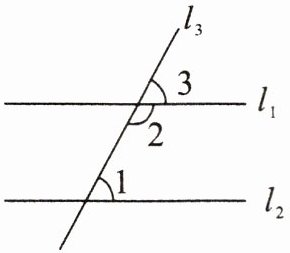
已知：如图,$l_{1}// l_{2}$,$l_{1}$,$l_{2}都被l_{3}$所截。
求证：$\angle 1+\angle 2 = 180^{\circ}$。
证明：假设$\angle 1+\angle 2$≠$180^{\circ}$。
$\because l_{1}// l_{2}$,$\therefore\angle 1$＝$\angle 3$。
$\because\angle 1+\angle 2$≠$180^{\circ}$,
$\therefore\angle 3+\angle 2eq180^{\circ}$,这和平角为180°矛盾,
$\therefore假设\angle 1+\angle 2$≠$180^{\circ}$不成立,
即$\angle 1+\angle 2 = 180^{\circ}$。

答案： ≠ ＝ ≠ 平角为180° ≠

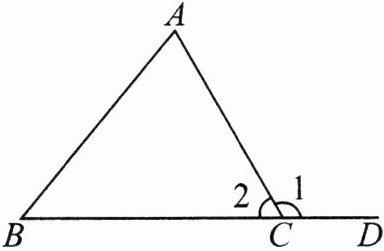
6. 用反证法求证：三角形的一个外角等于与它不相邻的两个内角的和。

答案： 解:已知:如图,∠1是△ABC的一个外角,求证:∠1=∠A+∠B.证明:假设∠1≠∠A+∠B,在△ABC中,∠A+∠B+∠2=180°,
∴∠A+∠B=180°-∠2.
∵∠1+∠2=180°,
∴∠1=180°-∠2.
∴∠1=∠A+∠B,与假设相矛盾,
∴假设不成立,
∴原命题成立,即∠1=∠A+∠B.

7. 阅读下列文字,回答问题。
在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle Aeq45^{\circ}$。
求证：$ACeq BC$。
证明：假设$AC = BC$。
$\because\angle Aeq45^{\circ}$,$\angle C = 90^{\circ}$,$\therefore\angle Aeq\angle B$。
$\because ACeq BC$,这与假设矛盾,$\therefore ACeq BC$。
上面的证明有没有错误？若没有错误,指出其证明的方法；若有错误,请予以纠正。

答案： 解:有错误.改正:假设AC=BC,则∠A=∠B,
∵∠C=90°,
∴∠B=∠A=45°,这与∠A≠45°矛盾,
∴AC=BC不成立,
∴AC≠BC.