第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. (1)多项式乘以多项式运算法则的依据是
乘法分配律
;
答案:
1.
(1)乘法分配律
(1)乘法分配律
(2)$(a + 4)(a + 3) = a \cdot a + a \cdot 3 + 4 \cdot$____$+ 4 × 3 = $____;
答案:
(2)a $a^{2}+7a+12$
(2)a $a^{2}+7a+12$
(3)$(2x - 5y)(3x - y) = 2x \cdot 3x + 2x \cdot$____$+ (-5y) \cdot 3x + (-5y) \cdot$____$=$____。
答案:
(3)
(3)
2. 计算$(a + 3)(-a + 1)$的结果是(
A.$-a^{2} - 2a + 3$
B.$-a^{2} + 4a + 3$
C.$-a^{2} + 4a - 3$
D.$a^{2} - 2a - 3$
A
)A.$-a^{2} - 2a + 3$
B.$-a^{2} + 4a + 3$
C.$-a^{2} + 4a - 3$
D.$a^{2} - 2a - 3$
答案:
2.A
3. 若$(x + 3)(x - 5) = x^{2} + mx - 15$,则$m$的值为(
A.$-2$
B.$2$
C.$-5$
D.$5$
【变式】如果$(x + m)与(x + 3)的乘积中不含x$的一次项,则$m$的值为
A
)A.$-2$
B.$2$
C.$-5$
D.$5$
【变式】如果$(x + m)与(x + 3)的乘积中不含x$的一次项,则$m$的值为
-3
。
答案:
3.A
@@【变式】-3
@@【变式】-3
4. 计算:
(1)$(m + 1)(2m - 1)$;
(2)$(2a - 3b)(3a + 2b)$;
(3)$(m - 1)(m^{2} + m + 1)$。
(1)$(m + 1)(2m - 1)$;
(2)$(2a - 3b)(3a + 2b)$;
(3)$(m - 1)(m^{2} + m + 1)$。
答案:
4.解:
(1)原式$=2m^{2}-m+2m-1=2m^{2}+m-1$;
(2)原式$=6a^{2}+4ab-9ab-6b^{2}=6a^{2}-5ab-6b^{2}$;
(3)原式$=m^{3}+m^{2}+m-m^{2}-m-1=m^{3}-1$.
(1)原式$=2m^{2}-m+2m-1=2m^{2}+m-1$;
(2)原式$=6a^{2}+4ab-9ab-6b^{2}=6a^{2}-5ab-6b^{2}$;
(3)原式$=m^{3}+m^{2}+m-m^{2}-m-1=m^{3}-1$.
5. (郑州期中改)若$3a^{2} - a - 3 = 0$,求$(3a + 5)(a - 2)$的值。
答案:
5.解:因为$3a^{2}-a-3=0$,
所以$3a^{2}-a=3$,
原式$=3a^{2}-6a+5a-10$
$=3a^{2}-a-10$
$=3-10$
$=-7$.
所以$3a^{2}-a=3$,
原式$=3a^{2}-6a+5a-10$
$=3a^{2}-a-10$
$=3-10$
$=-7$.
6. (教材展示问题变式)根据图①的面积可以说明多项式的乘法运算$(2a + b)(a + b) = 2a^{2} + 3ab + b^{2}$,那么根据图②的面积可以说明多项式的乘法运算是(
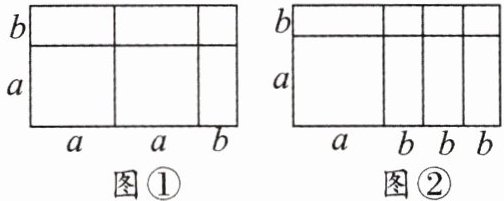
A.$(a + 3b)(a + b) = a^{2} + 4ab + 3b^{2}$
B.$(a + 3b)(a + b) = a^{2} + 3b^{2}$
C.$(b + 3a)(b + a) = b^{2} + 4ab + 3a^{2}$
D.$(a + 3b)(a - b) = a^{2} + 2ab - 3b^{2}$
A
)
A.$(a + 3b)(a + b) = a^{2} + 4ab + 3b^{2}$
B.$(a + 3b)(a + b) = a^{2} + 3b^{2}$
C.$(b + 3a)(b + a) = b^{2} + 4ab + 3a^{2}$
D.$(a + 3b)(a - b) = a^{2} + 2ab - 3b^{2}$
答案:
6.A
7. 将一块长为$a$,宽为$b$的长方形的长、宽分别增加$m$,$n$,下列表示这块长方形现在的面积的式子正确的是(
A.$an + bm + mn$
B.$(a + m)(b + n)$
C.$a(b + n) + b(a + m)$
D.$m(b + n) + n(a + m)$
B
)A.$an + bm + mn$
B.$(a + m)(b + n)$
C.$a(b + n) + b(a + m)$
D.$m(b + n) + n(a + m)$
答案:
7.B
8. 若一个三角形的底边长是$(2a + 6b)$,该底边上的高是$(4a - 5b)$,则这个三角形的面积是
$4a^{2}+7ab-15b^{2}$
。
答案:
8.$4a^{2}+7ab-15b^{2}$
查看更多完整答案,请扫码查看


