第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 下列描述属于定义的是(
A.两直线平行,内错角相等
B.三角形的内角和等于 $180^{\circ}$
C.对顶角相等
D.有一个角是直角的三角形叫作直角三角形
D
)A.两直线平行,内错角相等
B.三角形的内角和等于 $180^{\circ}$
C.对顶角相等
D.有一个角是直角的三角形叫作直角三角形
答案:
D
2. 两条直线相交成直角,就叫作两条直线互相垂直,这个句子是
定义
.(填“定义”或“命题”)
答案:
定义
3. 下面关于基本事实和定理的联系的说法不正确的是(
A.基本事实和定理都是真命题
B.基本事实就是定理,定理就是基本事实
C.基本事实和定理都可以作为推理论证的依据
D.基本事实的正确性不需证明,定理的正确性需证明
B
)A.基本事实和定理都是真命题
B.基本事实就是定理,定理就是基本事实
C.基本事实和定理都可以作为推理论证的依据
D.基本事实的正确性不需证明,定理的正确性需证明
答案:
B
4. 下列语句中,属于定理的是(
A.在直线 $AB$ 上取一点 $E$
B.如果两个角相等,那么这两个角是对顶角
C.同位角相等
D.同角的补角相等
D
)A.在直线 $AB$ 上取一点 $E$
B.如果两个角相等,那么这两个角是对顶角
C.同位角相等
D.同角的补角相等
答案:
D
5. 如图,直线 $AB$,$CD$ 被直线 $DE$ 所截,$AB$ 与 $CD$ 相交于点 $F$,当 $\angle D+\angle EFB = 180^{\circ}$ 时,$AB// DC$.
(1)$\because\angle EFA+\angle EFB = 180^{\circ}$,$\angle D+\angle EFB = 180^{\circ}$,$\therefore\angle D= \angle EFA$,$\therefore AB// DC$,所依据的基本事实或定理是:
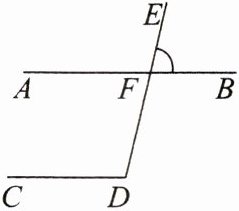
(2)$\because\angle EFB= \angle AFD$,$\angle D+\angle EFB = 180^{\circ}$,$\therefore\angle D+\angle AFD = 180^{\circ}$,$\therefore AB// DC$,所依据的基本事实或定理是:
(1)$\because\angle EFA+\angle EFB = 180^{\circ}$,$\angle D+\angle EFB = 180^{\circ}$,$\therefore\angle D= \angle EFA$,$\therefore AB// DC$,所依据的基本事实或定理是:
同位角相等,两直线平行
;
(2)$\because\angle EFB= \angle AFD$,$\angle D+\angle EFB = 180^{\circ}$,$\therefore\angle D+\angle AFD = 180^{\circ}$,$\therefore AB// DC$,所依据的基本事实或定理是:
同旁内角互补,两直线平行
.
答案:
(1)同位角相等,两直线平行
(2)同旁内角互补,两直线平行
(1)同位角相等,两直线平行
(2)同旁内角互补,两直线平行
6. 下面关于“证明”的说法正确的是(
A.“证明”是一种命题
B.“证明”是一种定理
C.“证明”是一种推理过程
D.“证明”就是举例说明
C
)A.“证明”是一种命题
B.“证明”是一种定理
C.“证明”是一种推理过程
D.“证明”就是举例说明
答案:
C
7. 推理:如图,$\because\angle AOC= \angle BOD$,$\therefore\angle AOC+\angle AOB= \angle BOD+\angle AOB$,这个推理的依据是(
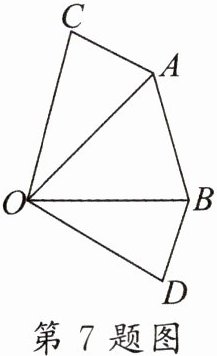
A.等量加等量和相等
B.等量减等量差相等
C.等量代换
D.整体大于部分
A
)
A.等量加等量和相等
B.等量减等量差相等
C.等量代换
D.整体大于部分
答案:
A
8. 根据题图,完成下列推理过程.
(1)$\because\angle 1= \angle A$(已知),$\therefore AD// BC$;(
(2)$\because\angle 3= \angle 4$(已知),$\therefore DC// AB$;(
(3)$\because\angle 2= \angle 5$(已知),$\therefore AD// BC$;(
(4)$\because\angle ADC+\angle C = 180^{\circ}$(已知),$\therefore AD// BC$.(
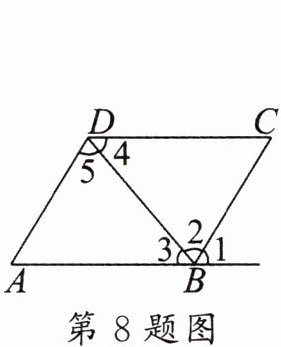
(1)$\because\angle 1= \angle A$(已知),$\therefore AD// BC$;(
同位角相等,两直线平行
)(2)$\because\angle 3= \angle 4$(已知),$\therefore DC// AB$;(
内错角相等,两直线平行
)(3)$\because\angle 2= \angle 5$(已知),$\therefore AD// BC$;(
内错角相等,两直线平行
)(4)$\because\angle ADC+\angle C = 180^{\circ}$(已知),$\therefore AD// BC$.(
同旁内角互补,两直线平行
)
答案:
(1)同位角相等,两直线平行
(2)内错角相等,两直线平行
(3)内错角相等,两直线平行
(4)同旁内角互补,两直线平行
(1)同位角相等,两直线平行
(2)内错角相等,两直线平行
(3)内错角相等,两直线平行
(4)同旁内角互补,两直线平行
9. 如图,已知 $AD\perp BC$,$EF\perp BC$,$\angle 1= \angle 2$.求证:$DG// BA$.
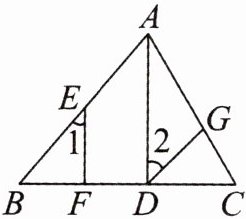

答案:
证明:
∵AD⊥BC,EF⊥BC(已知),
∴AD//EF(垂直于同一直线的两直线平行),
∴∠1=∠BAD(两直线平行,同位角相等).又
∵∠1=∠2(已知),
∴∠2=∠BAD(等量代换),
∴DG//BA(内错角相等,两直线平行).
∵AD⊥BC,EF⊥BC(已知),
∴AD//EF(垂直于同一直线的两直线平行),
∴∠1=∠BAD(两直线平行,同位角相等).又
∵∠1=∠2(已知),
∴∠2=∠BAD(等量代换),
∴DG//BA(内错角相等,两直线平行).
查看更多完整答案,请扫码查看


