第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 如图,小明作∠AOB的平分线的步骤如下:
①以点O为圆心,适当长为半径作弧,交OA于点M,交OB于点N;
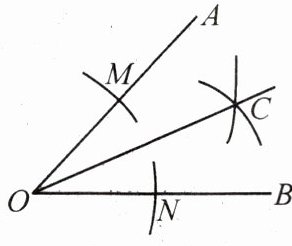
②分别以点M,N为圆心,大于$\frac{1}{2}MN$的长为半径作弧,两弧在∠AOB的内部相交于点C。
③作射线OC;
小明作图的依据是(
A.SSS
B.ASA
C.SAS
D.HL
①以点O为圆心,适当长为半径作弧,交OA于点M,交OB于点N;

②分别以点M,N为圆心,大于$\frac{1}{2}MN$的长为半径作弧,两弧在∠AOB的内部相交于点C。
③作射线OC;
小明作图的依据是(
A
)A.SSS
B.ASA
C.SAS
D.HL
答案:
A
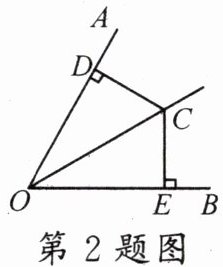
2. 如图,C为∠AOB平分线上的一点,CD⊥OA于点D,CE⊥OB于点E,若CD= 6,则CE的长为(
A.3
B.5
C.6
D.9
C
)
A.3
B.5
C.6
D.9
答案:
C
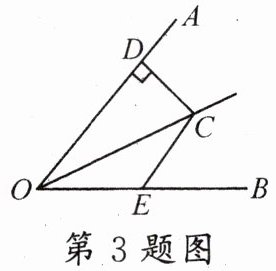
3. 新考向 一题多问(漯河三中开学卷改)如图,C是∠AOB平分线上的一点,CD⊥OA于点D,E是边OB上的一动点,若CD= 4,则:
(1)CE长度的取值范围是(
A.CE<4 B.CE>4 C.CE≥4 D.CE≤4
(2)若OE= 6,则△COE的面积为
(1)CE长度的取值范围是(
C
)A.CE<4 B.CE>4 C.CE≥4 D.CE≤4
(2)若OE= 6,则△COE的面积为
12
。
答案:
(1)C
(2)12
(1)C
(2)12
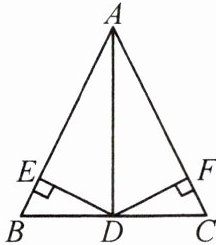
4. 如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,且BE= CF,求证:BD= CD。

答案:
证明:
∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴∠BED = ∠CFD = 90°,DE = DF.
在△BDE和△CDF中,
BE = CF,
∠BED = ∠CFD,
DE = DF,
∴△BDE ≌ △CDF(SAS).
∴BD = CD.
∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴∠BED = ∠CFD = 90°,DE = DF.
在△BDE和△CDF中,
BE = CF,
∠BED = ∠CFD,
DE = DF,
∴△BDE ≌ △CDF(SAS).
∴BD = CD.
5. 新课标 过程学习 如图,PC⊥OA,PD⊥OB,当PC= PD时,Rt△OPC≌Rt△
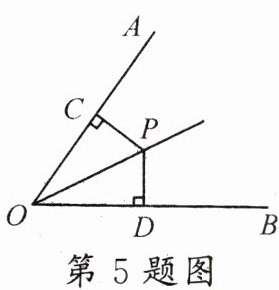
OPD
(HL),∴∠POC= ∠POD
。
答案:
OPD POD
6. 两个完全一样的三角板如图摆放,使三角板的一条直角边分别与△ABC的边AB,AC重合,它们的顶点重合于点M,则点M一定在(
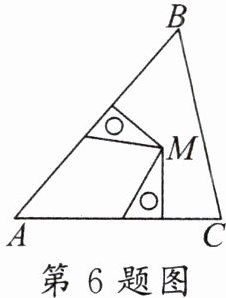
A.∠A的平分线上
B.AC边的高上
C.BC边的中垂线上
D.AB边的中线上
A
)
A.∠A的平分线上
B.AC边的高上
C.BC边的中垂线上
D.AB边的中线上
答案:
A
7. 如图,已知点P到BE,BD,AC的距离恰好相等,则点P的位置:①在∠B的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠B,∠DAC,∠ECA三个角的平分线的交点.上述结论中,正确的结论为
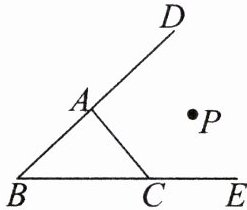
①②③④
。
答案:
①②③④
8. 已知:如图,∠B= ∠C= 90°,M是BC的中点,DM平分∠ADC.求证:AM平分∠DAB.
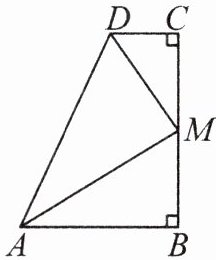

答案:
证明:过点M作ME⊥AD,垂足为E.
∵DM平分∠ADC,
∴∠CDM = ∠EDM.
∵MC⊥CD,ME⊥AD,
∴ME = MC.
又
∵M是BC的中点,
∴MC = MB,
∴ME = MB.
∵MB⊥AB,ME⊥AD,
∴AM平分∠DAB.

证明:过点M作ME⊥AD,垂足为E.
∵DM平分∠ADC,
∴∠CDM = ∠EDM.
∵MC⊥CD,ME⊥AD,
∴ME = MC.
又
∵M是BC的中点,
∴MC = MB,
∴ME = MB.
∵MB⊥AB,ME⊥AD,
∴AM平分∠DAB.

查看更多完整答案,请扫码查看


