第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
12.(淮阳区期末)已知x没有平方根,且$\vert x\vert=64,$则x的立方根为
A.8
B.-8
C.±4
D.-4
-4
A.8
B.-8
C.±4
D.-4
答案:
12.D
13.$\sqrt[3]{(-8)^{3}}的立方根是-2$
A.8
B.-8
C.2
D.-2
D
A.8
B.-8
C.2
D.-2
答案:
13.D
14.正方体$M的体积是正方体N$的体积的64倍,那么正方体$M的棱长是正方体N的棱长的4$倍
A.4倍
B.8倍
C.16倍
D.2倍
A
A.4倍
B.8倍
C.16倍
D.2倍
答案:
14.A
15.(河南省实验中学月考)若$a^{2}= 16,\sqrt[3]{-b}= -2,$则a + b的值
A.12
B.12或4
C.12或±4
D.-12或4
B
A.12
B.12或4
C.12或±4
D.-12或4
答案:
15.B
16.(汝阳期中)若$\sqrt[3]{3m - 7}和\sqrt[3]{3n + 4}$互为相反数,则$m + n = $
1
答案:
16.1
17.若$x + 17$的立方根是3,则$3x - 5$的平方根是
±5
答案:
17.±5
18.求下列各式中的$x$的值:
(1)$x^{3}= -8$,$x = - 2$;
(2)$(x - 3)^{3}= 64$,$x - 3 = 4$,$x = 7$;
(3)$\frac{1}{3}x^{3}-\frac{1}{8}= 1$,$\frac{1}{3}x^{3}= \frac{9}{8}$,$x^{3}= \frac{27}{8}$,$x= \frac{3}{2}$;
(4)$(x + 3)^{3}+27 = 0$,$(x + 3)^{3}= -27$,$x + 3= -3$,$x= -6$。
(1)$x^{3}= -8$,$x = - 2$;
(2)$(x - 3)^{3}= 64$,$x - 3 = 4$,$x = 7$;
(3)$\frac{1}{3}x^{3}-\frac{1}{8}= 1$,$\frac{1}{3}x^{3}= \frac{9}{8}$,$x^{3}= \frac{27}{8}$,$x= \frac{3}{2}$;
(4)$(x + 3)^{3}+27 = 0$,$(x + 3)^{3}= -27$,$x + 3= -3$,$x= -6$。
答案:
18.解:
(1)x=-2;
(2)x=7;
(3)$x=\frac{3}{2}$;
(4)x=-6.
(1)x=-2;
(2)x=7;
(3)$x=\frac{3}{2}$;
(4)x=-6.
19.如图,一个长方体水箱的长、宽、高之比为$2:2:4$,其体积为$16000cm^{3}$。
(1)求长方体水箱的长、宽、高;
(2)当把一个半径为$r cm$的铁球放入注满水的水箱中,溢出水池外的水的体积为水池体积的$\frac{1}{60}$,求该小球的半径。($\pi$取3,结果精确到$0.01cm$)
(1)求长方体水箱的长、宽、高;
(2)当把一个半径为$r cm$的铁球放入注满水的水箱中,溢出水池外的水的体积为水池体积的$\frac{1}{60}$,求该小球的半径。($\pi$取3,结果精确到$0.01cm$)
答案:
19.解:
(1)设长方体水箱的长、宽、高分别为2x,2x,4x,所以2x·2x·4x=16 000,所以$x^3=1 000$,解得x=10.所以长方体水箱的长、宽、高分别为20 cm,20 cm,40 cm;
(2)因为该小球的半径为r cm,则$\frac{4}{3}\pi r^3=\frac{1}{60}×16 000$,所以$r^3=\frac{1}{60}×16 000×\frac{1}{4}\pi$,所以r≈4.05.故该小球的半径约为4.05 cm.
(1)设长方体水箱的长、宽、高分别为2x,2x,4x,所以2x·2x·4x=16 000,所以$x^3=1 000$,解得x=10.所以长方体水箱的长、宽、高分别为20 cm,20 cm,40 cm;
(2)因为该小球的半径为r cm,则$\frac{4}{3}\pi r^3=\frac{1}{60}×16 000$,所以$r^3=\frac{1}{60}×16 000×\frac{1}{4}\pi$,所以r≈4.05.故该小球的半径约为4.05 cm.
20.信息理解题:
(1)填表:
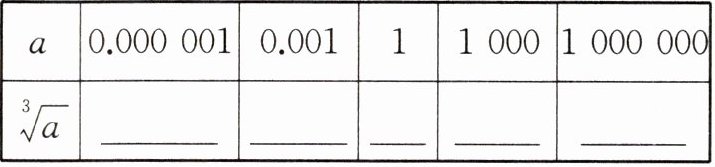
(2)由上表可发现什么规律?请用语言叙述这个规律:被开方数的小数点每向右(或向左)移动三位,它的立方根的小数点相应地向右(或向左)移动一位。
(3)根据你发现的规律填空:
①已知$\sqrt[3]{3}= 1.442$,则$\sqrt[3]{3000}=$
②已知$\sqrt[3]{456}= 7.697$,$\sqrt[3]{0.456}=$
(1)填表:

0.01 0.1 1 10 100
(2)由上表可发现什么规律?请用语言叙述这个规律:被开方数的小数点每向右(或向左)移动三位,它的立方根的小数点相应地向右(或向左)移动一位。
(3)根据你发现的规律填空:
①已知$\sqrt[3]{3}= 1.442$,则$\sqrt[3]{3000}=$
14.42
,$\sqrt[3]{0.003}=$0.014 42
;②已知$\sqrt[3]{456}= 7.697$,$\sqrt[3]{0.456}=$
0.769 7
。
答案:
20.
(1)0.01 0.1 1 10 100
(2)被开方数的小数点向左(右)移动三位,立方根结果的小数点向左(右)移动一位
(3)①14.42 0.014 42 ②0.769 7
(1)0.01 0.1 1 10 100
(2)被开方数的小数点向左(右)移动三位,立方根结果的小数点向左(右)移动一位
(3)①14.42 0.014 42 ②0.769 7
查看更多完整答案,请扫码查看


