第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
9. 如图,在△ABC 中,点 D 在边 BC 上,DE⊥AB 于点 E,DF⊥BC 交 AC 于点 F,且 BD = CF,BE = CD。若∠EDF = 70°,则∠AFD 的度数为 (
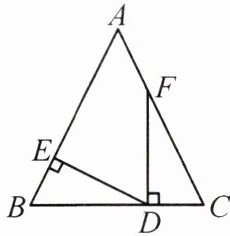
A.160°
B.150°
C.140°
D.120°
A
)
A.160°
B.150°
C.140°
D.120°
答案:
A
10. 如图,D 为 Rt△ABC 的斜边 BC 上的一点,且 BD = AB,DE⊥BC 交 AC 于点 E。若 AC = 11,DE = 4,则 CE =

7
。
答案:
7
11. 思想方法分类讨论如图,在 Rt△ABC 中,∠C = 90°,AC = 16 cm,BC = 8 cm,射线 AD⊥AC,线段 PQ = AB,其两端点 P,Q 分别在射线 AC 和射线 AD 上移动,点 P 从点 A 开始移动,速度为 2 cm/s,则当点 P 运动
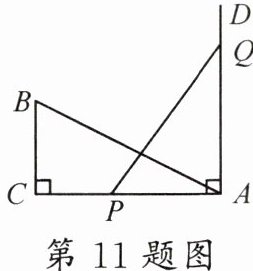
4或8
s 时,△ABC 和△APQ 全等。
答案:
4或8
12. (教材练习题变式)如图,在△ABC 中,D 是 BC 的中点,DE⊥AB 于点 E,DF⊥AC 于点 F,且 BE = CF。求证:
(1)DE = DF;(2)AB = AC。

(1)DE = DF;(2)AB = AC。

答案:
(1)
∵D是BC的中点,
∴BD=CD.
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
又
∵BE=CF,
∴Rt△BDE≌Rt△CDF(HL).
∴DE=DF;
(2)连结AD.由
(1)可知DE=DF,
又
∵AD=AD,
∴Rt△ADE≌Rt△ADF(HL).
∴AE=AF.
又
∵BE=CF,
∴AE+BE=AF+CF,即AB=AC.
(1)
∵D是BC的中点,
∴BD=CD.
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
又
∵BE=CF,
∴Rt△BDE≌Rt△CDF(HL).
∴DE=DF;
(2)连结AD.由
(1)可知DE=DF,
又
∵AD=AD,
∴Rt△ADE≌Rt△ADF(HL).
∴AE=AF.
又
∵BE=CF,
∴AE+BE=AF+CF,即AB=AC.
13. 新课标综合与实践【知识再现】
学完本课后,我们知道“斜边和一直角边分别相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”)”是判定直角三角形全等的特有方法。
【简单应用】
(1)如图①,在△ABC 中,∠A = 90°,AB = AC,点 D,E 分别在边 AC,AB 上,且 BD = CE,则线段 AD 和线段 AE 之间的数量关系为
【拓展延伸】
(2)若将(1)中的条件“∠A = 90°”改为“∠A 为钝角”,其他条件不变,如图②,(1)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由。

学完本课后,我们知道“斜边和一直角边分别相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”)”是判定直角三角形全等的特有方法。
【简单应用】
(1)如图①,在△ABC 中,∠A = 90°,AB = AC,点 D,E 分别在边 AC,AB 上,且 BD = CE,则线段 AD 和线段 AE 之间的数量关系为
AD=AE
,请说明理由;【拓展延伸】
(2)若将(1)中的条件“∠A = 90°”改为“∠A 为钝角”,其他条件不变,如图②,(1)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由。

答案:
(1)AD=AE.理由如下:
在Rt△ABD和Rt△ACE中,{AB=AC,BD=CE}
∴Rt△ABD≌Rt△ACE(HL).
∴AD=AE;
(2)成立.
证明:分别过点B,C作
BF⊥CA交CA的延长线
于点F,CG⊥BA交BA的延长线于点G,则∠F=∠G=90°.
∠BAF=∠CAG,
在△ABF和△ACG中,{∠BAF=∠CAG,∠F=∠G,AB=AC}
∴△ABF≌△ACG(AAS).
∴AF=AG,BF=CG.
在Rt△BDF和Rt△CEG中,{BD=CE,BF=CG}
∴Rt△BDF≌Rt△CEG(HL).
∴EG=DF.
又
∵AG=AF,
∴EG−AG=DF−AF,即AE=AD.
∴AD=AE.
(1)AD=AE.理由如下:
在Rt△ABD和Rt△ACE中,{AB=AC,BD=CE}
∴Rt△ABD≌Rt△ACE(HL).
∴AD=AE;
(2)成立.
证明:分别过点B,C作
BF⊥CA交CA的延长线
于点F,CG⊥BA交BA的延长线于点G,则∠F=∠G=90°.
∠BAF=∠CAG,
在△ABF和△ACG中,{∠BAF=∠CAG,∠F=∠G,AB=AC}
∴△ABF≌△ACG(AAS).
∴AF=AG,BF=CG.
在Rt△BDF和Rt△CEG中,{BD=CE,BF=CG}
∴Rt△BDF≌Rt△CEG(HL).
∴EG=DF.
又
∵AG=AF,
∴EG−AG=DF−AF,即AE=AD.
∴AD=AE.
查看更多完整答案,请扫码查看


