第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. $\sqrt{625}$的算术平方根是(
A.25
B.$\pm 25$
C.5
D.$\pm 5$
C
)A.25
B.$\pm 25$
C.5
D.$\pm 5$
答案:
C
2. 下列计算正确的是(
A.$\sqrt[3]{\dfrac{27}{8}}= \dfrac{3}{2}$
B.$\sqrt{25}= \pm 5$
C.$-(-2)^{2}= 4$
D.$\sqrt{(-4)^{2}}= -4$
A
)A.$\sqrt[3]{\dfrac{27}{8}}= \dfrac{3}{2}$
B.$\sqrt{25}= \pm 5$
C.$-(-2)^{2}= 4$
D.$\sqrt{(-4)^{2}}= -4$
答案:
A
3. 已知$x$,$y$为实数,且$\sqrt{x - 3}+(y + 2)^{2}= 0$,则$y^{x}$的立方根是(
A.$\sqrt[3]{6}$
B.$-8$
C.$-2$
D.$\pm 2$
C
)A.$\sqrt[3]{6}$
B.$-8$
C.$-2$
D.$\pm 2$
答案:
C
4. 一个正偶数的算术平方根是$a$,那么与这个正偶数相邻的下一个正偶数的算术平方根是(
A.$a + 2$
B.$a^{2}+2$
C.$\sqrt{a^{2}+2}$
D.$\sqrt{a + 2}$
C
)A.$a + 2$
B.$a^{2}+2$
C.$\sqrt{a^{2}+2}$
D.$\sqrt{a + 2}$
答案:
C
5. 求下列各式的值:
(1) $-\sqrt{1\dfrac{7}{9}}$;
(2) $-\sqrt[3]{1-\dfrac{37}{64}}$.
(1) $-\sqrt{1\dfrac{7}{9}}$;
(2) $-\sqrt[3]{1-\dfrac{37}{64}}$.
答案:
解:
(1)原式$=-\frac{4}{3}$;
(2)原式$=-\frac{3}{4}$.
(1)原式$=-\frac{4}{3}$;
(2)原式$=-\frac{3}{4}$.
6. 已知$4a + 1的平方根是\pm 3$,$b - 1的立方根为2$.
(1) 求$a与b$的值;
(2) 求$2a + b + 3$的平方根.
(1) 求$a与b$的值;
(2) 求$2a + b + 3$的平方根.
答案:
解:
(1)因为$4a + 1$的平方根是$\pm 3$,所以$4a + 1=9$,解得$a=2$.因为$b - 1$的立方根为2,所以$b - 1=8$,解得$b=9$;
(2)因为$a=2$,$b=9$,所以$2a + b + 3=2× 2 + 9 + 3=16$,所以$2a + b + 3$的平方根是$\pm 4$.
(1)因为$4a + 1$的平方根是$\pm 3$,所以$4a + 1=9$,解得$a=2$.因为$b - 1$的立方根为2,所以$b - 1=8$,解得$b=9$;
(2)因为$a=2$,$b=9$,所以$2a + b + 3=2× 2 + 9 + 3=16$,所以$2a + b + 3$的平方根是$\pm 4$.
7. (郑州模拟)下列实数是无理数的是(
A.$\sqrt{4}$
B.$\dfrac{\pi}{3}$
C.$5$
D.$3.14$
B
)A.$\sqrt{4}$
B.$\dfrac{\pi}{3}$
C.$5$
D.$3.14$
答案:
B
8. 下列各数:$\dfrac{22}{7}$,$0$,$3.\dot{6}\dot{6}$,$\dfrac{\pi}{2}$,$-\dfrac{1}{3}$,$-0.232\ 332…$(每两个$2之间依次多一个3$),$64$,$4^{2}$,$\sqrt{9}$,$\sqrt[3]{8}$,$-\sqrt{2}$中,无理数的个数有
3
个.
答案:
3
9. 我国是最早认识和使用负数的国家,下列各数中,最大的负数是(
A.$0$
B.$-1$
C.$-\sqrt{2}$
D.$-2$
B
)A.$0$
B.$-1$
C.$-\sqrt{2}$
D.$-2$
答案:
B
10. 如图,表示$-\sqrt{7}$的点落在(
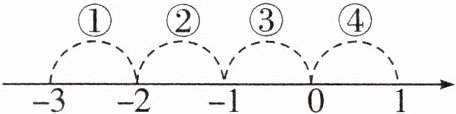
A.段①
B.段②
C.段③
D.段④
]
A
)
A.段①
B.段②
C.段③
D.段④
]
答案:
A
11. 下列各组有理数的大小比较中,正确的是(
A.$-(-1)<-(+2)$
B.$-|-3|>-(-2)$
C.$-\pi<-3.14$
D.$-(-0.3)<-\left|-\dfrac{1}{3}\right|$
C
)A.$-(-1)<-(+2)$
B.$-|-3|>-(-2)$
C.$-\pi<-3.14$
D.$-(-0.3)<-\left|-\dfrac{1}{3}\right|$
答案:
C
12. (河南月考)已知$\sqrt{11}+1在两个连续的自然数a和a + 1$之间,$1是b$的一个平方根.
(1) 求$a$,$b$的值;
(2) 比较$a + b的算术平方根与3$的大小.
(1) 求$a$,$b$的值;
(2) 比较$a + b的算术平方根与3$的大小.
答案:
解:
(1)因为$9<11<16$,所以$3<\sqrt{11}<4$.又因为$\sqrt{11}+1$在两个连续的自然数$a$和$a + 1$之间,$1$是$b$的一个平方根,所以$a=4$,$b=1$;
(2)由
(1)知,$a=4$,$b=1$,所以$a + b=4 + 1=5$,所以$a + b$的算术平方根是$\sqrt{5}$.因为$5<9$,所以$\sqrt{5}<3$.
(1)因为$9<11<16$,所以$3<\sqrt{11}<4$.又因为$\sqrt{11}+1$在两个连续的自然数$a$和$a + 1$之间,$1$是$b$的一个平方根,所以$a=4$,$b=1$;
(2)由
(1)知,$a=4$,$b=1$,所以$a + b=4 + 1=5$,所以$a + b$的算术平方根是$\sqrt{5}$.因为$5<9$,所以$\sqrt{5}<3$.
查看更多完整答案,请扫码查看


