《2025年课堂点睛九年级数学上册人教版宁夏专版》

10.如图,△ABC中,∠ABC= 90°,AB= 2,AC= 4,点O为BC的中点,以O为圆心,以OB为半径作半圆,交AC于点D,则图中阴影部分的面积是$\frac{5\sqrt{3}}{4}-\frac{\pi}{2}$.

答案： $\frac{5\sqrt{3}}{4}-\frac{\pi}{2}$

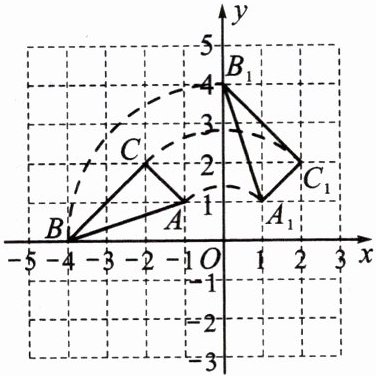
11.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-1,1),B(-4,0),C(-2,2).将△ABC绕原点O顺时针旋转90°后得到$△A_1B_1C_1.$
(1)请写出$A_1、$$B_1、$$C_1$三点的坐标;
(2)求点B旋转到点$B_1$的弧长.

答案：
(1)由图知，$A_{1}(1,1)$，$B_{1}(0,4)$，$C_{1}(2,2)$。　
(2)由题意知，点B旋转到点$B_{1}$的弧所在的圆的半径为4，弧所对的圆心角为$90^{\circ}$，
∴弧长为：$\frac{90\pi×4}{180}=2\pi$。

12.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF= 1,BC= $2\sqrt{3}$,求阴影部分的面积.

答案：

(1)证明:连接OC.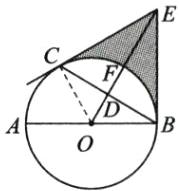
∵CE与$\odot O$相切于点C，
∴$\angle OCE = 90^{\circ}$，
∵$OC = OB$，$OD\perp BC$，
∴$\angle EOC = \angle EOB$，在$\triangle EOC$和$\triangle EOB$中，$\begin{cases} OC = OB \\ \angle EOC = \angle EOB \\ OE = OE \end{cases}$，
∴$\triangle EOC\cong\triangle EOB(SAS)$，
∴$\angle OCE = \angle OBE$，
∴$\angle OBE = 90^{\circ}$，
∴BE与$\odot O$相切。
(2)解:$S_{阴影}=4\sqrt{3}-\frac{4}{3}\pi$。

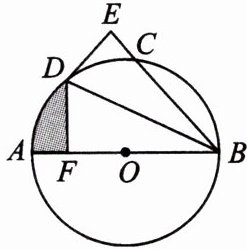
13.(核心素养·几何直观)(宝鸡市一中模拟)如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE= $3\sqrt{3}$,DF= 3,求图中阴影部分的面积.

答案：

(1)DE与$\odot O$相切，理由:连接DO，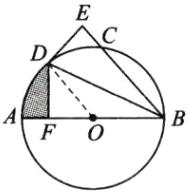
∵$DO = BO$，
∴$\angle ODB = \angle OBD$。
∵$\angle ABC$的平分线交$\odot O$于点D，
∴$\angle EBD = \angle DBO$，
∴$\angle EBD = \angle BDO$，
∴$DO// BE$。
∵$DE\perp BC$，
∴$DE\perp DO$，
∴DE与$\odot O$相切。
(2)
∵BD平分$\angle ABC$，$DE\perp BE$，$DF\perp AB$，
∴$DE = DF = 3$。
∵$BE = 3\sqrt{3}$，
∴$BD = \sqrt{DE^{2}+BE^{2}}=\sqrt{3^{2}+(3\sqrt{3})^{2}} = 6$，
∴$\angle DBA = \angle DBE = 30^{\circ}$，
∴$\angle DOF = 60^{\circ}$，
∴$DO = 2\sqrt{3}$，$FO = \sqrt{3}$，故图中阴影部分的面积为$S_{扇形AOD}-S_{\triangle FOD}=\frac{60\pi×(2\sqrt{3})^{2}}{360}-\frac{1}{2}×\sqrt{3}×3 = 2\pi-\frac{3\sqrt{3}}{2}$。