《2025年课堂点睛九年级数学上册人教版宁夏专版》

1.下列关于二次函数$y= 3(x+1)(2-x)$的图象和性质的叙述中,正确的是 (D)
A.点$(0,2)$在函数图象上
B.开口方向向上
C.对称轴是直线$x= 1$
D.与直线$y= 3x$有两个交点

答案： D

2.(宁波市中考)点$A(m-1,y_{1})$,$B(m,y_{2})都在二次函数y= (x-1)^{2}+n$的图象上.若$y_{1}＜y_{2}$,则$m$的取值范围为 (B)
A.$m＞2$
B.$m＞\frac{3}{2}$
C.$m＜1$
D.$\frac{3}{2}＜m＜2$

答案： B

3.在平面直角坐标系中,将抛物线$y= x^{2}+2x-1先绕原点旋转180^{\circ}$,再向下平移5个单位,所得到的抛物线的顶点坐标是(1,-3).

答案： (1,-3)

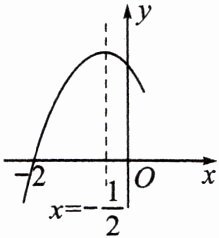
4.(贵港市中考)已知二次函数$y= ax^{2}+bx+c(a≠0)$图象的一部分如图所示,该函数图象经过点$(-2,0)$,对称轴为直线$x= -\frac{1}{2}$.对于下列结论：①$abc＜0$；②$b^{2}-4ac＞0$；③$a+b+c= 0$；④$am^{2}+bm＜\frac{1}{4}(a-2b)$(其中$m≠-\frac{1}{2}$)；⑤若$A(x_{1},y_{1})和B(x_{2},y_{2})$均在该函数图象上,且$x_{1}＞x_{2}＞1$,则$y_{1}＞y_{2}$.其中正确结论的个数共有3个.

答案： 3

5.抛物线的函数解析式为$y= (x-2)^{2}-9$,则下列结论中,正确的序号为 (B)
①当$x= 2$时,$y取得最小值-9$；②若点$(3,y_{1})$,$(4,y_{2})$在其图象上,则$y_{2}＞y_{1}$；③将其函数图象向左平移3个单位长度,再向上平移4个单位长度所得抛物线的函数解析式为$y= (x-5)^{2}-5$；④函数图象与$x$轴有两个交点,且两交点的距离为6.
A.②③④
B.①②④
C.①③
D.①②③④

答案： B

6.(无锡市中考)把二次函数$y= x^{2}+4x+m$的图象向上平移1个单位长度,再向右平移3个单位长度,如果平移后所得抛物线与坐标轴有且只有一个公共点,那么$m$应满足条件m＞3.

答案： m＞3

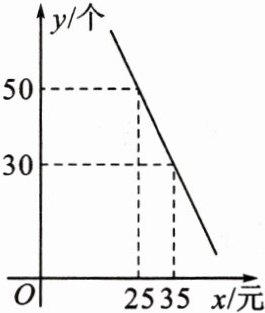
7.(盘锦市中考)某商场新进一批拼装玩具,进价为每个10元,在销售过程中发现,日销售量$y$(个)与销售单价$x$(元)之间满足如图所示的一次函数关系.
(1)求$y与x$的函数关系式(不要求写出自变量$x$的取值范围)；
(2)若该玩具某天的销售利润是600元,则当天玩具的销售单价是多少元？
(3)设该玩具日销售利润为$w$元,当玩具的销售单价定为多少元时,日销售利润最大？最大利润是多少元？

答案： 解:
(1)设一次函数的关系式为y=kx+b,由题图可知,函数图象过点(25,50)和点(35,30),把这两点的坐标代入一次函数y=kx+b,得{25k+b=50,35k+b=30,解得{k=-2,b=100,
∴一次函数的关系式为y=-2x+100.
(2)根据题意,设当天玩具的销售单价是x元,由题意,得(x-10)×(-2x+100)=600.解得x1=40,x2=20,
∴当天玩具销售单价为40元或20元.
(3)根据题意,则w=(x-10)×(-2x+100),整理,得w=-2(x-30)²+800,
∵-2＜0,
∴当x=30时,w有最大值,最大值为800,
∴当玩具销售单价定为30元时,日销售利润最大,最大利润为800元.