第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
旋转的概念:把一个图形绕着某一点O转动一个角度的图形变换叫做旋转.点O叫做①
旋转的性质:(1)对应点到旋转中心的距离②
中心对称:把一个图形绕着某一个点旋转⑤
中心对称的性质:(1)关于中心对称的两个图形,对称点所连线段都经过⑦
中心对称图形:把一个图形绕着某一个点旋转⑩
关于原点对称的点的坐标:两个点关于原点对称时,它们的坐标符号⑫
旋转中心
,转动的角叫做旋转角.旋转的性质:(1)对应点到旋转中心的距离②
相等
;(2)对应点与旋转中心所连线段形成的夹角等于③旋转角
;(3)旋转前、后的图形④全等
.中心对称:把一个图形绕着某一个点旋转⑤
$180^{\circ}$
,如果它能够与另一个图形⑥重合
,那么就说这两个图形关于这个点对称或中心对称.中心对称的性质:(1)关于中心对称的两个图形,对称点所连线段都经过⑦
对称中心
,而且被对称中心⑧平分
;(2)关于中心对称的两个图形⑨全等
.中心对称图形:把一个图形绕着某一个点旋转⑩
$180^{\circ}$
,如果旋转后的图形能够与原来的图形⑪重合
,那么这个图形叫做中心对称图形,这个点就是它的对称中心.关于原点对称的点的坐标:两个点关于原点对称时,它们的坐标符号⑫
相反
,即点P(x,y)关于原点的对称点为P'⑬$(-x,-y)$
.
答案:
①旋转中心;②相等;③旋转角;④全等;⑤$180^{\circ}$;⑥重合;⑦对称中心;⑧平分;⑨全等;⑩$180^{\circ}$;⑪重合;⑫相反;⑬$(-x,-y)$。
1.(天津市中考)如图,在△ABC中,AB= AC,若M是BC边上任意一点,将△ABM绕点A逆时针旋转得到△ACN,点M的对应点为点N,连接MN,则下列结论一定正确的是(
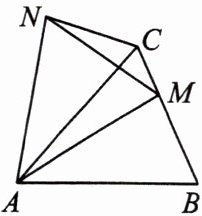
A.AB= AN
B.AB//NC
C.∠AMN= ∠ACN
D.MN⊥AC
C
)
A.AB= AN
B.AB//NC
C.∠AMN= ∠ACN
D.MN⊥AC
答案:
C
2.(大武口区模拟)如图,将等边△AOB放在平面直角坐标系中,点A的坐标为(0,4),点B在第一象限,将等边△AOB绕点O顺时针旋转75°得到△A'OB',则点B'的坐标是
$(2\sqrt{2},-2\sqrt{2})$
.
答案:
$(2\sqrt{2},-2\sqrt{2})$
3.(西宁市中考)如图,在△ABC中,∠C= 90°,∠B= 30°,AB= 6,将△ABC绕点A逆时针方向旋转15°得到△AB'C',B'C'交AB于点E,则B'E=
$3\sqrt{3}-3$
.
答案:
$3\sqrt{3}-3$
4.如图,正方形ABCD的边长等于2,它绕顶点B按顺时针方向旋转得到正方形A'BC'D'.在这个过程中:
(1)旋转中心是点______;
(2)若旋转角为45°,边CD与A'D'交于点F,求DF的长度.

(1)旋转中心是点______;
(2)若旋转角为45°,边CD与A'D'交于点F,求DF的长度.

答案:
4.
(1)B
(2)解:连接BD,

∵旋转角为$45^{\circ}$,$\therefore \angle ABA'=45^{\circ}$.
∵四边形ABCD为正方形,$\therefore \angle ABD=45^{\circ}$.$\therefore \angle ABA'=\angle ABD$.
∴点B,A',D三点在一条直线上,$\angle A'DF=45^{\circ}$.在$Rt\triangle ABD$中,$BD=\sqrt{AB^{2}+AD^{2}}=\sqrt{2^{2}+2^{2}}=2\sqrt{2}$.$\because A'D=BD-BA'$,$\therefore A'D=2\sqrt{2}-2$.在$Rt\triangle A'DF$中,$A'F=A'D=2\sqrt{2}-2$,$\therefore DF=\sqrt{A'D^{2}+A'F^{2}}=\sqrt{2}A'D=4-2\sqrt{2}$.
4.
(1)B
(2)解:连接BD,

∵旋转角为$45^{\circ}$,$\therefore \angle ABA'=45^{\circ}$.
∵四边形ABCD为正方形,$\therefore \angle ABD=45^{\circ}$.$\therefore \angle ABA'=\angle ABD$.
∴点B,A',D三点在一条直线上,$\angle A'DF=45^{\circ}$.在$Rt\triangle ABD$中,$BD=\sqrt{AB^{2}+AD^{2}}=\sqrt{2^{2}+2^{2}}=2\sqrt{2}$.$\because A'D=BD-BA'$,$\therefore A'D=2\sqrt{2}-2$.在$Rt\triangle A'DF$中,$A'F=A'D=2\sqrt{2}-2$,$\therefore DF=\sqrt{A'D^{2}+A'F^{2}}=\sqrt{2}A'D=4-2\sqrt{2}$.
查看更多完整答案,请扫码查看


