《2025年课堂点睛九年级数学上册人教版宁夏专版》

11. 如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且$CF\perp AD$.
(1)求证：点E是OB的中点；
(2)若$AB= 8$,求CD的长.

答案：
(1)证明：连接AC，
∵AB是⊙O的直径，AB⊥CD，
∴CE=DE，即AB垂直平分CD，
∴AC=AD，△ACD是等腰三角形。
∵CF⊥AD，AB⊥CD，
∴∠AFC=∠AED=90°。
又
∵∠FAO=∠EAD，
∴△AOF∽△ADE，
∴∠AOF=∠ADE。
∵∠AOF=∠COE，∠ADE=∠ACE（同弧所对圆周角相等），
∴∠COE=∠ACE。
又
∵∠CEO=∠AEC=90°，
∴△COE∽△ACE，
∴$\frac{OE}{CE}=\frac{CE}{AE}$，即$CE^2=OE\cdot AE$。
设⊙O的半径为r，OE=x，则AE=r+x，CE²=r² - x²（勾股定理），
∴$r^2 - x^2 = x(r + x)$，
化简得$r^2 - rx - 2x^2 = 0$，即$(r - 2x)(r + x)=0$，
∵r + x≠0，
∴r=2x，即OE=$\frac{r}{2}$，
∵OB=r，
∴BE=OB - OE=r - $\frac{r}{2}$=$\frac{r}{2}$=OE，
∴点E是OB的中点。
(2)解：
∵AB=8，
∴⊙O的半径r=4，
由
(1)知OE=$\frac{r}{2}$=2，
在Rt△COE中，CE=$\sqrt{OC^2 - OE^2}=\sqrt{4^2 - 2^2}=\sqrt{12}=2\sqrt{3}$，
∵AB⊥CD，
∴CD=2CE=4$\sqrt{3}$。
答案：
(1)见证明过程；
(2)CD的长为$4\sqrt{3}$。

12. (核心素养·应用意识)(汉中市龙岗中学模拟)如图,某地有一座圆弧形的拱桥,圆弧所在圆的圆心为O,半径为OC,桥下水面宽AB为$7.2\mathrm{m}$,拱顶C高出水面$2.4\mathrm{m}$($CD= 2.4\mathrm{m}$),现有一艘宽$3\mathrm{m}$,船舱顶部为正方形并高出水面$2\mathrm{m}$的货船要经过这里,此时货船能顺利通过这座拱桥吗？请说明理由.

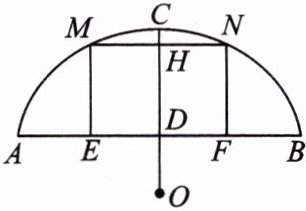
答案：
解:能顺利通过.理由:由题意得AB=7.2m,CD=2.4m,连接AO、NO.设⊙O的半径为Rm,在Rt△AOD中,OD=(R - 2.4)m,AD=3.6m,
∴R²=(R - 2.4)²+3.6²,
∴R=3.9m.在Rt△OHN中,若HN= $\frac{1}{2}$MN=1.5m,则OH= $\sqrt{ON^2 - HN^2}$= $\sqrt{3.9^2 - 1.5^2}$=3.6(m).
∵OD=OC - CD=3.9 - 2.4=1.5(m),
∴DH=OH - OD=3.6 - 1.5=2.1(m),NF=ME=HD=2.1m＞2m,
∴此时货船能顺利通过.

1. 如图,$\odot O$的半径为5,半径OD垂直于弦AB于点C,$AD= 2\sqrt{5}$,则AB的长为8.

答案： 8

2. 如图,$\odot O$的直径AB和弦CD相交于点E,$AE= 1\mathrm{cm}$,$\odot O的半径为3\mathrm{cm}$,$\angle DEB= 60^\circ$,则CD的长为2$\sqrt{6}$$\mathrm{cm}$.

答案： 2$\sqrt{6}$