第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是(
A.96
B.69
C.66
D.99
B
)A.96
B.69
C.66
D.99
答案:
B
2. (南充市中考)如图,将直角三角板ABC绕顶点A顺时针旋转到△AB'C',点B'恰好落在CA的延长线上,∠B= 30°,∠C= 90°,则∠BAC'为(
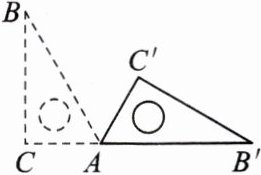
A.90°
B.60°
C.45°
D.30°
B
)
A.90°
B.60°
C.45°
D.30°
答案:
B
3. 如图所示,△AOB绕着点O旋转至△A'OB',此时:
(1)点B的对应点是
(2)旋转中心是
(3)∠A的对应角是
(1)点B的对应点是
点B'
;(2)旋转中心是
点O
,旋转角为∠AOA'或∠BOB'
;(3)∠A的对应角是
∠A'
,线段OB的对应线段是线段OB'
.
答案:
(1)点B'
(2)点O ∠AOA'或∠BOB'
(3)∠A' OB'
(1)点B'
(2)点O ∠AOA'或∠BOB'
(3)∠A' OB'
4. 如图,将△ABC绕点C逆时针旋转得到△A'B'C,其中点A'与A是对应点,点B'与B是对应点,点B'落在边AC上,连接A'B,若∠ACB= 45°,AC= 3,BC= 2,则A'B的长为
$\sqrt{13}$
.
答案:
$\sqrt{13}$
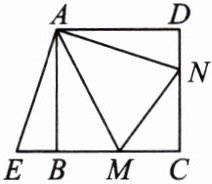
5. 如图,点M,N分别在正方形ABCD的边BC,CD上,且∠MAN= 45°,把△ADN绕点A顺时针旋转90°得到△ABE.
(1)求证:△AEM≌△ANM.
(2)若BM= 3,DN= 2,求正方形ABCD的边长.
(1)求证:△AEM≌△ANM.
(2)若BM= 3,DN= 2,求正方形ABCD的边长.

答案:
(1)证明:由旋转的性质得,$\triangle ADN\cong\triangle ABE$,$\therefore\angle DAN=\angle BAE$,$AE=AN$,$\angle D=\angle ABE=90^\circ$,$\therefore\angle ABC+\angle ABE=180^\circ$,$\therefore$点E,点B,点C三点共线.$\because\angle DAB=90^\circ$,$\angle MAN=45^\circ$,$\therefore\angle MAE=\angle BAE+\angle BAM=\angle DAN+\angle BAM=45^\circ$,$\therefore\angle MAE=\angle MAN$.$\because MA=MA$,$\therefore\triangle AEM\cong\triangle ANM(\text{SAS})$.
(2)解:设$CD=BC=x$,则$CM=x-3$,$CN=x-2$,$\because\triangle AEM\cong\triangle ANM$,$\triangle ADN\cong\triangle ABE$,$\therefore EM=MN$,$BE=DN$,$\therefore MN=BM+DN=5$.$\because\angle C=90^\circ$,$\therefore MN^2=CM^2+CN^2$,$\therefore5^2=(x-2)^2+(x-3)^2$,解得,$x=6$或$-1$(舍去).$\therefore$正方形ABCD的边长为6.
(1)证明:由旋转的性质得,$\triangle ADN\cong\triangle ABE$,$\therefore\angle DAN=\angle BAE$,$AE=AN$,$\angle D=\angle ABE=90^\circ$,$\therefore\angle ABC+\angle ABE=180^\circ$,$\therefore$点E,点B,点C三点共线.$\because\angle DAB=90^\circ$,$\angle MAN=45^\circ$,$\therefore\angle MAE=\angle BAE+\angle BAM=\angle DAN+\angle BAM=45^\circ$,$\therefore\angle MAE=\angle MAN$.$\because MA=MA$,$\therefore\triangle AEM\cong\triangle ANM(\text{SAS})$.
(2)解:设$CD=BC=x$,则$CM=x-3$,$CN=x-2$,$\because\triangle AEM\cong\triangle ANM$,$\triangle ADN\cong\triangle ABE$,$\therefore EM=MN$,$BE=DN$,$\therefore MN=BM+DN=5$.$\because\angle C=90^\circ$,$\therefore MN^2=CM^2+CN^2$,$\therefore5^2=(x-2)^2+(x-3)^2$,解得,$x=6$或$-1$(舍去).$\therefore$正方形ABCD的边长为6.
查看更多完整答案,请扫码查看


