《2025年课堂点睛九年级数学上册人教版宁夏专版》

1. 若一个四边形的外接圆与内切圆是同心圆,则这个四边形一定是 (C)
A.矩形
B.菱形
C.正方形
D.不能确定

答案： C

2. 一个正多边形的中心角为30°,这个正多边形的边数是 (D)
A.3
B.6
C.8
D.12

答案： D

3.(青岛市中考)如图,正六边形ABCDEF内接于⊙O,点M在$\overset{\frown }{AB}$上,则∠CME的度数为 (D)
A.30°
B.36°
C.45°
D.60°

答案： 解：连接OC、OE。
∵正六边形ABCDEF内接于⊙O，
∴∠COE=360°÷6×2=120°。
∵点M在$\overset{\frown }{AB}$上，
∴∠CME=$\frac{1}{2}$∠COE=60°。
答案：D

4.(长春市中考)跳棋是一项传统的智力游戏,如图是一副跳棋棋盘的示意图,它可以看作是由全等的等边三角形ABC和等边三角形DEF组合而成,它们重叠部分的图形为正六边形. 若AB= 27厘米,则这个正六边形的周长为54厘米.

答案： 解：设正六边形的边长为 $ x $ 厘米。
因为正六边形的各边相等，且它是由两个全等的等边三角形重叠而成，所以等边三角形 $ ABC $ 的边长 $ AB $ 可表示为 $ 3x $（正六边形的边长与三角形边上未重叠部分的线段长相等，每条边上有两段未重叠部分和一段重叠部分，共三段）。
已知 $ AB = 27 $ 厘米，所以 $ 3x = 27 $，解得 $ x = 9 $。
正六边形的周长为 $ 6x = 6×9 = 54 $ 厘米。
54

5. 如图所示,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若A点的坐标为(-1,0),则点C的坐标为$(\frac {1}{2}，-\frac {\sqrt{3}}{2})$.

答案： $(\frac {1}{2}，-\frac {\sqrt{3}}{2})$

6. 已知圆的半径是6,则圆内接正三角形的边长是$6\sqrt{3}$.

答案： 【解析】：
本题主要考查正多边形与圆的关系，特别是正三角形内接于圆时的边长计算。
设圆内接正三角形为$\bigtriangleup ABC$，圆心为$O$，半径为$6$。
由于是正三角形，所以圆心$O$到三角形三个顶点的距离都等于圆的半径，即$OA = OB = OC = 6$。
考虑圆心$O$到三角形一边（例如$AB$）的垂线$OD$，由于是正三角形，$OD$也是$AB$边上的中垂线。
在直角三角形$OAD$中，$OA = 6$，$\angle OAD = 30^\circ$（因为正三角形的内角为$60^\circ$，所以其一半为$30^\circ$）。
利用三角函数或特殊角的三角函数值，我们有$AD = OA × \cos(30^\circ) = 6 × \frac{\sqrt{3}}{2} = 3\sqrt{3}$。
因此，正三角形的边长$AB = 2 × AD = 2 × 3\sqrt{3} = 6\sqrt{3}$。
【答案】：
$6\sqrt{3}$。

7. 如图,已知正三角形ABC的边长为6,求它的中心角、半径和边心距.

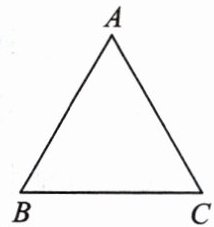
答案： 【解析】：本题主要考查正多边形与圆的关系，特别是正三角形与其外接圆的相关性质。
对于正三角形，其中心角是由正多边形的边数决定的，公式为$\frac{360^{\circ}}{n}$，其中$n$为正多边形的边数。
正三角形的半径$R$可以通过正弦定理求得，即$R=\frac{a}{2\sin\frac{\pi}{3}}$，其中$a$为正三角形的边长。
边心距$r$是正三角形的中心到边的垂直距离，可以通过半径$R$和正三角形的高来求得，也可以通过三角函数关系直接求得。
【答案】：解：
中心角：
由于是正三角形，所以中心角为$\frac{360^{\circ}}{3}=120^{\circ}$。
半径：
正三角形的边长为6，所以半径$R$可以通过正弦定理求得，
$R=\frac{6}{2\sin60^{\circ}}=\frac{6}{\sqrt{3}}=2\sqrt{3}$，
边心距：
边心距$r$是正三角形的中心到边的垂直距离，
$r=R\cos30^{\circ}=2\sqrt{3}×\frac{\sqrt{3}}{2}= \sqrt{3}$，
所以，正三角形ABC的中心角为$120^{\circ}$，半径为$2\sqrt{3}$，边心距为$\sqrt{3}$。

8. 若AB是⊙O内接正五边形的一边,AC是⊙O的内接正六边形的一边,则∠BAC等于6°或114°.

答案： 解：
情况一：点C在劣弧AB上。
连接OA、OB、OC。
∵AB是⊙O内接正五边形的一边，
∴∠AOB=360°÷5=72°。
∵AC是⊙O内接正六边形的一边，
∴∠AOC=360°÷6=60°。
∴∠BOC=∠AOB - ∠AOC=72° - 60°=12°。
∵OA=OB=OC，
∴∠OAB=∠OBA=(180° - ∠AOB)÷2=(180° - 72°)÷2=54°，
∠OAC=∠OCA=(180° - ∠AOC)÷2=(180° - 60°)÷2=60°。
∴∠BAC=∠OAC - ∠OAB=60° - 54°=6°。
情况二：点C在优弧AB上。
连接OA、OB、OC。
∠AOB=72°，∠AOC=60°。
∠BOC=∠AOB + ∠AOC=72° + 60°=132°。
∠OAB=54°，∠OAC=60°。
∠BAC=∠OAB + ∠OAC=54° + 60°=114°。
综上，∠BAC等于6°或114°。
答案：6°或114°

9. 在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受到了中国人的浪漫. 如图,将“雪花”图案(边长为4的正六边形ABCDEF)放在平面直角坐标系中,若AB与x轴垂直,顶点A的坐标为(2,-3),则顶点C的坐标为 (A)
A.(2-2$\sqrt{3}$,3)
B.(0,1+2$\sqrt{3}$)
C.(2-$\sqrt{3}$,3)
D.(2-2$\sqrt{3}$,2+$\sqrt{3}$)

答案： 解：
∵正六边形ABCDEF边长为4，AB⊥x轴，A(2,-3)，
∴AB在过点A且垂直于x轴的直线上，AB=4，B点在A点上方，
∴B点坐标为(2,-3+4)=(2,1)。
连接OA、OB、OC，正六边形中心为O，OA=OB=OC=4，∠AOB=∠BOC=60°，
∴△OAB为等边三角形，OA=AB=4，
过O作OH⊥AB于H，H为AB中点，
∴H点坐标为(2,(-3+1)/2)=(2,-1)，OH=√(OA²-AH²)=√(4²-2²)=2√3。
∵AB⊥x轴，OH⊥AB，
∴OH//x轴，
∵H(2,-1)，OH=2√3且O在H左侧，
∴O点坐标为(2-2√3,-1)。
∠BOC=60°，OB在y轴右侧（B(2,1)），OC与OB夹角60°，
OB方向向量为(2-(2-2√3),1-(-1))=(2√3,2)，
旋转OB 60°得OC方向，
OC终点C坐标：O点坐标+OC向量，
OC向量模长4，与x轴夹角：arctan(2/(2√3))=30°，旋转60°后为30°+60°=90°，
∴OC在y轴正方向，OC长度4，
∴C点坐标为(2-2√3,-1+4)=(2-2√3,3)。
答案：A