《2025年课堂点睛九年级数学上册人教版宁夏专版》

10. 已知二次函数 $ y= 5(x-a)^2 $,当 $ x＞4 $ 时,$ y $ 随 $ x $ 的增大而增大,则 $ a $ 的取值范围是a≤4.

答案： a≤4

11. 如图所示是一座古拱桥的截面图,拱桥桥洞的水上部分是抛物线形状,当水面的宽度为 10m 时,桥洞与水面的最大距离是 5m. 经过讨论,同学们得出如下三种建立平面直角坐标系的方案：


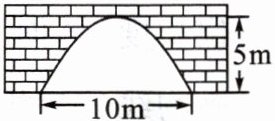
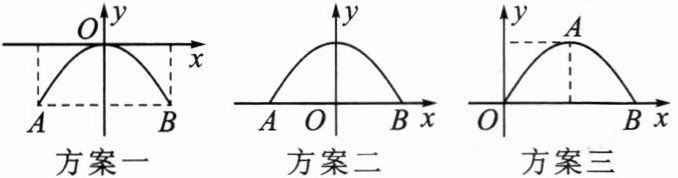
请你结合题意回答下列问题：
(1) 求出方案一的函数解析式；
(2) 方案二,方案三的函数图象可以看成由方案一怎样平移得到的？
(3) 因为上游水库泄洪,水面宽度变为 6m,求水面上涨的高度.

答案：
(1)设y=ax²,把x=5,y=−5代入得a=−$\frac{1}{5}$,
∴y=−$\frac{1}{5}$x².　　
(2)方案二可以看作由方案一中的抛物线向上平移5个单位长度得到的;方案三可以看作再由方案二向右平移5个单位长度得到的.　
(3)把x=3代入y=−$\frac{1}{5}$x²,得y=−$\frac{9}{5}$=−1.8,
∴水面上涨的高度为5−1.8=3.2(m).

12. (核心素养·几何直观)(铜川阳光中学期中)如图是二次函数 $ y= (x+2)^2 $ 的图象,顶点为 A,与 y 轴的交点为 B.
(1) 求经过 A、B 两点的直线的函数关系式.
(2) 请在第二象限中的抛物线上找一点 C,使$ \triangle ABC $ 的面积与 $ \triangle ABO $ 的面积相等.

答案：
(1)令x=0,则y=2²=4,
∴B(0,4).令y=0,则(x+2)²=0,
∴x1=x2=−2.
∴A(−2,0).设过A,B两点的直线的函数关系式为y=kx+b,由题意，得$\begin{cases} 0=-2k+b, \\ 4=b. \end{cases}$解得$\begin{cases} k=2, \\ b=4. \end{cases}$
∴经过A,B两点的直线的函数关系式为y=2x+4.　
(2)由题意,得S△AOB=$\frac{1}{2}$AO·BO=$\frac{1}{2}$×2×4=4.过点C 作CD⊥x轴于点D,设C(m,n),则n=(m+2)²,
∴CD=(m+2)²,DO=−m,DA=−2−m.
∴S△ABC=S梯形CDOB−S△CDA−S△AOB=−$\frac{m}{2}$[(m+2)²+4]−$\frac{1}{2}$(−2−m)(m+2)²−4=m²+2m.
∵S△ABC=S△AOB=4,
∴m²+2m=4.解得m1=−1+$\sqrt{5}$(不合题意,舍去),m2=−1-$\sqrt{5}$.
∴C(−1−$\sqrt{5}$,6−2$\sqrt{5}$).